TianyaoBlogs
0%

PHYS 5120 - Computational Energy Materials and Electronic Structure Simulations-W7-1

发表于 更新于 分类于

PHYS 5120 - 计算能源材料和电子结构模拟 Lecture

Lecturer: Prof.PAN DING

I:

这些内容共同构成了量子化学中用于计算分子电子结构的基石——Hartree-Fock (HF) 自洽场 (SCF) 方法。

核心概念：Hartree-Fock (HF) 近似

  • 目标：求解多电子体系（如分子）的薛定谔方程。但这个方程非常复杂，无法精确求解。
  • 核心思想 (HF 近似)：
    1. 波恩-奥本海默近似：假定原子核固定不动，我们只关心电子的运动。
    2. 单电子近似：这是 HF 近似最关键的一步。它假设每个电子的运动只受到一个“平均场”的影响，这个平均场是由原子核和其他所有电子共同产生的。
    3. 反对称性：电子是费米子，必须满足泡利不相容原理。HF 方法通过一个称为“斯莱特行列式 (Slater Determinant)”的数学工具来构造总波函数，以自动满足这个要求。

⬅基本算符与方程

1. Hartree-Fock 方程：f̂ |φi> = εi |φi>

它在形式上是一个本征方程。

  • |φi> (分子轨道)：这是我们要求解的第 i 个单电子波函数（或称为轨道）。
  • f̂ (Fock 算符)：这是一个等效的单电子哈密顿算符。它代表了一个电子在原子核和所有其他电子的“平均场”中所感受到的总能量。
  • εi (轨道能量)：这是第 i 个分子轨道的能量，即电子占据该轨道时的能量。

2. Fock 算符的构成：f̂ = ĥ₁(r) + Σ[j] (2Ĵj(r) - K̂j(r))

这个公式详细定义了 Fock 算符 f̂ 是由什么组成的。

  • ĥ₁(r) (核心哈密顿算符)：这是“单电子”部分，与电子间的相互作用无关。它只包括：
    1. 电子的动能：白板上的 -(ħ²/2m)∇² 项。
    2. 电子与所有原子核的吸引势能：白板上的 -Σ[I] (Z_I e² / |r - R_I|) 项。
  • Σ[j] (2Ĵj(r) - K̂j(r)) (双电子相互作用)：这是描述电子 i 与其他所有电子 j 之间平均相互作用的项（求和 Σ[j] 遍历所有被占据的轨道）。
    • Ĵj(r) (库仑算符)：
      • 物理意义：描述了电子 i 与轨道 j 上的电子云（密度为 |φj|²）之间的经典静电排斥。
      • 白板上的定义：Ĵj(ψ) = <φj | e² / |r - r'| | φj> ψ。这意味着 Ĵj 作用在一个函数 ψ(r) 上时，它会计算 ψ(r) 与 φj(r') 之间的平均排斥能。
    • K̂j(r) (交换算符)：
      • 物理意义：这是一个纯粹的量子力学效应，没有经典对应。它源于波函数的反对称性要求（泡利不相容原理）。它修正了电子“自我排斥”的错误（因为 Ĵj 包含了 j=i 的情况），并降低了自旋平行电子相遇的概率，从而降低了能量。
      • 白板上的定义：K̂j(ψ) = <φj | e² / |r - r'| | ψ> φj。注意 ψ 和 φj 在积分符号内的位置发生了“交换”，因此得名。
    • 系数 “2”：在闭壳层（Closed-Shell）HF 方法中，我们假设每个分子轨道 j 都被两个自旋相反的电子（一个自旋向上 α，一个自旋向下 β）占据。因此，Ĵj 的排斥作用要乘以 2。而 K̂j 的交换作用只发生在自旋相同的电子之间，因此只有一个 K̂j 被减去（例如，自旋向上的电子 i 只与自旋向上的电子 j 发生交换）。

3. HOMO / LUMO

  • HOMO (Highest Occupied Molecular Orbital)：最高占据分子轨道。这是 HF 计算得到的 εi 能量中，能量最高但仍被电子占据的那个轨道。
  • LUMO (Lowest Unoccupied Molecular Orbital)：最低未占分子轨道。这是 εi 能量中，能量最低但没有电子占据的那个轨道。
  • 意义：HOMO 和 LUMO 统称为“前线轨道”。它们的能量差（HOMO-LUMO Gap）和形状在化学反应中至关重要，决定了分子倾向于从哪里给出电子 (HOMO) 和从哪里接受电子 (LUMO)。

矩阵化 (Roothaan-Hall 方法)

直接求解上面的 Hartree-Fock 方程（它是微分-积分方程）非常困难。C. C. J. Roothaan 和 G. G. Hall 提出了一种将其转换为标准矩阵代数问题的方法。

1. LCAO 展开

我们假设未知的分子轨道 |φi> 可以由一组已知的原子轨道 (Atomic Orbitals, AOs) |χμ> 线性组合而成： |φi> = Σ[μ] Cμi |χμ> 其中 Cμi 是我们要解的系数。

2. Roothaan-Hall 方程：F C = S C ε

这是将 LCAO 展开代入 HF 方程后得到的矩阵方程。

  • F (Fock 矩阵)：Fμν = <χμ | f̂ | χν>。这是 Fock 算符 f̂ 在原子轨道基组下的矩阵表示。
  • C (系数矩阵)：矩阵的每一列 i 都是一个分子轨道 φi 的展开系数 Cμi。
  • S (重叠矩阵)：Sμν = <χμ | χν>。它描述了原子轨道基函数之间的重叠程度。如果基函数是“正交”的，S 就是单位矩阵。
  • ε (轨道能量矩阵)：这是一个对角矩阵，对角线上的元素 εi 就是我们要求的分子轨道能量。

3. Fock 矩阵元的计算：Fμν = Hμν^core + Gμν

这是求解的核心，它把 F 矩阵的计算分为两部分：

  • ① Hμν^core = <χμ | ĥ₁ | χν> (核心哈密顿矩阵元)：
    • 物理意义：这是“单电子”部分，只包含电子动能和电子-原子核吸引能。
    • 计算：这部分在整个计算过程中只用计算一次，因为它不依赖于电子的分布。
  • Gμν (双电子积分项)：
    • 物理意义：这是“双电子”排斥部分，对应于 Σ[j] (2Ĵj - K̂j)。
    • 问题：计算 Gμν 需要知道库仑和交换算符，而这些算符又依赖于分子轨道 |φj>，而 |φj> 又是由我们要求解的系数 C 决定的。这就形成了一个“鸡生蛋，蛋生鸡”的循环问题。

4. 密度矩阵与 SCF 循环

为了解决这个循环问题，我们引入了密度矩阵 P。

  • ③ 密度矩阵 (Density Matrix) P：
    • 白板上的定义：Pαβ = 2 Σ[j=1 to N/2] Cαj* Cβj
    • 物理意义：P 描述了电子在原子轨道基组上的分布情况。它由系数矩阵 C 构造。
  • 使用 P 构建 Fock 矩阵 F：
    • 白板上的公式：Fμν = Hμν^core + Σ[αβ] Pαβ * (...) （白板上 (...) 部分代表了 (μν|αβ) - 1/2(μα|νβ) 这样的双电子积分项）。
    • 关键点：F 矩阵（代表电子间的相互作用）现在被表示为密度矩阵 P（代表电子的分布）的函数。F = F(P)。

总结：自洽场 (SCF) 的完整流程

完整地描述了 “自洽场” (Self-Consistent Field, SCF) 的计算流程：

  1. 第 0 步：选择原子轨道基组 |χμ>，并计算所有不变的积分，如重叠矩阵 S 和核心哈密顿矩阵 H^core。
  2. 第 1 步 (猜测)：对系数矩阵 C 做一个初始猜测（例如，通过一个更简单的方法得到），并用它来构建一个初始的密度矩阵 P^(0)。
  3. 第 2 步 (构建)：使用当前的密度矩阵 P^(k) 来构建 Fock 矩阵 F^(k)。 Fμν = Hμν^core + Gμν(P^(k))
  4. 第 3 步 (求解)：求解 Roothaan-Hall 矩阵方程 F^(k) C^(k+1) = S C^(k+1) ε^(k+1)，得到一组新的系数矩阵 C^(k+1) 和新的轨道能量 ε^(k+1)。
  5. 第 4 步 (更新)：使用新的系数 C^(k+1) 来计算一个新的密度矩阵 P^(k+1)。
  6. 第 5 步 (检查自洽)：比较新的密度矩阵 P^(k+1) 和旧的密度矩阵 P^(k)。
    • 如果 P^(k+1) 和 P^(k) 几乎相同（即“自洽”了），说明我们找到的电子分布 P 所产生的“平均场” F，反过来再求解这个 F 得到的电子分布恰好就是 P 本身。计算收敛，循环结束。
    • 如果它们不相同，就令 k = k+1，返回第 2 步，用新的 P 继续迭代。

这个迭代过程，就是 Hartree-Fock 自洽场方法的核心。

II:

两个关键部分：

  1. 1.：继续详细推导如何使用密度矩阵 (Density Matrix) 来构建 Fock 矩阵中的双电子相互作用项。
  2. 2.：展示了如何从数学上求解 Roothaan-Hall 方程 (F C = S C ε)，这是一个“广义本征值问题”，并将其转换为计算机可以轻松处理的“标准本征值问题”。

Fock 矩阵元的最终形式

这部分是整个 HF-SCF 方法中最核心的数学推导之一。它展示了如何将复杂的双电子相互作用（Gμν）表示为密度矩阵 P 和一堆预先计算好的积分的乘积。

  • Pαβ = 2 Σ[j=1 to N/2] Cαj* Cβj
    • 重申密度矩阵 P 的定义。它由系数矩阵 C 构建。
  • 推导 ③：<χμ | Σ[j] ... | χν>
    • 这一长串推导（从 ③ 开始，一直到 = Σ[αβ] Pαβ (...)）是白板上最复杂的部分。
    • 目标：计算 Fock 矩阵的双电子部分 Gμν = <χμ | Σ[j] (2Ĵj - K̂j) | χν>。
    • 步骤：
      1. 将分子轨道 |φj> 用原子轨道 |χ> 展开：|φj> = Σ[α] Cαj |χα>。
      2. 将这个展开式代入 Ĵj 和 K̂j 的积分定义中。
      3. 这会产生涉及四个原子轨道基函数的积分，称为双电子积分 (Two-Electron Integrals)，通常写作 (μν|αβ)。
      4. 经过复杂的代数重排（将 C 和 Σ[j] 重新组合），推导发现 Gμν 可以被写成： Gμν = Σ[αβ] Pαβ * [ (μν|αβ) - 1/2 (μα|νβ) ]
        • (μν|αβ) 是库仑积分。
        • (μα|νβ) 是交换积分。
  • Fμν = Hμν^core + Σ[αβ] Pαβ (...)
    • 最终的 Fock 矩阵元公式。
    • Fμν（Fock 矩阵）= Hμν^core（核心哈密顿矩阵，只算一次）+ Gμν（双电子排斥项）。
    • 关键在于 Gμν 是密度矩阵 P 的线性函数。
    • 这完美地建立了 SCF 的循环关系：C → P → F → 求解 F 得到新的 C。

Roothaan-Hall 方程的求解问题

这部分转向了一个纯粹的数学（线性代数）问题：如何求解我们建立的矩阵方程。

  • S† F C = C ε (笔误)
    • 白板上划掉的 S† F C = C ε 及其旁边的推导 (S†F)† = ... 看起来像是一个错误的尝试或旁注，试图探索这个矩阵的厄米性 (Hermiticity)。
    • 正确的方程（在它下面）是 F C = S C ε。
  • F C = S C ε (Roothaan-Hall 方程)
    • 问题：这不是一个“标准本征值问题” (A x = λ x)，因为在等式右边多了一个重叠矩阵 S。S 不是单位矩阵 I，因为原子轨道基组 |χ> 通常不是正交的。
    • 术语：这被称为“广义本征值问题”。
  • S is positive definite (S 是正定矩阵)
    • 这是一个关键的数学性质。S 是正定的，意味着它所有的本征值（λi）都大于零。
    • 意义：因为 S 是正定的，所以它保证是可逆的（S⁻¹ 存在），并且我们可以对它进行“开方”，即找到 S^(1/2) 和 S^(-1/2)。
  • S = R† R 或 S = U† Λ U (S 的分解)
    • 这是对 S 矩阵进行对角化或分解的标准方法。
    • S = U† Λ U 是谱分解：
      • U 是 S 的本征向量矩阵。
      • Λ 是由 S 的本征值 λi 组成的对角矩阵。
  • S^(1/2) = U† √Λ U 和 S^(-1/2) = U† (1/√Λ) U
    • （右侧白板上有 S^(-1/2) 的定义）。
    • 这是利用 S 的分解来定义它的 1/2 次方和 -1/2 次方矩阵。√Λ 就是简单地将对角矩阵 Λ 上的每个元素 λi 都开方。

变换为标准本征值问题

这部分展示了如何利用 S^(-1/2) 矩阵来“清除”方程中的 S，将其变为标准本征值问题。这个过程称为正交化 (Orthogonalization)。

  1. 目标：将 F C = S C ε 变换为 F' C' = C' ε 的形式。
  2. 定义新的系数矩阵 C'： 我们定义一组新的、在正交化基组下的系数 C'，它与原始系数 C 的关系是： C' = S^(1/2) C （因此 C = S^(-1/2) C'）
  3. 代入原方程： 将 C = S^(-1/2) C' 代入 F C = S C ε： F (S^(-1/2) C') = S (S^(-1/2) C') ε
  4. 两边左乘 S^(-1/2)： (S^(-1/2) F S^(-1/2)) C' = (S^(-1/2) S S^(-1/2)) C' ε
  5. 简化：
    • 右侧：如白板所示，S^(-1/2) S S^(-1/2) = S^(-1/2) S^(1/2) S^(1/2) S^(-1/2) = I（单位矩阵）。
    • 左侧：我们定义一个新的、变换后的 Fock 矩阵 F'： F' = S^(-1/2) F S^(-1/2)
  6. 最终的标准本征值方程： F' C' = C' ε

总结：SCF 循环的完整计算步骤

一个完整的 SCF 迭代步骤如下：

  1. 猜测 C^(0) (或 P^(0))。
  2. 构建 P：使用 C^(k) 计算密度矩阵 P^(k)。
  3. 构建 F：使用 P^(k) 构建 Fock 矩阵 F^(k)（如左侧推导所示）。
  4. 构建 F’：使用 S^(-1/2)（它在计算开始前就算好了）和 F^(k) 来构建变换后的 Fock 矩阵 F'^(k) = S^(-1/2) F^(k) S^(-1/2)。
  5. 求解：F'^(k) C'^(k+1) = C'^(k+1) ε^(k+1)。这是一个标准本征值问题，计算机可以高效求解，得到新的 C' 和 ε。
  6. 反变换：通过 C^(k+1) = S^(-1/2) C'^(k+1) 得到我们真正的系数矩阵 C。
  7. 检查收敛：用 C^(k+1) 计算新的 P^(k+1)，与 P^(k) 比较。如果不收敛，返回第 2 步。

在数学上解决了如何在非正交基组下求解 HF 方程的实际计算问题。

III:

两个主要部分：

  1. 上部：完成 Roothaan-Hall 方程的数学求解变换。
  2. 下部：引入一个全新且至关重要的概念——Hartree-Fock (HF) 的总能量。

方程的最终求解形式

“标准本征值问题”变换的总结和补充。

  • S^(-1/2) = U† (1/√λ ... 0; 0 ... 1/λ_m) U
    • 这是 S^(-1/2) 矩阵的明确计算方法，即通过对重叠矩阵 S 进行“谱分解”：
      1. 对角化 S 得到其本征向量矩阵 U 和本征值对角矩阵 Λ (对角元为 λ_i)。
      2. 计算 Λ^(-1/2)（即把每个 λ_i 替换为 1/√λ_i）。
      3. 重新组合 U† Λ^(-1/2) U 得到 S^(-1/2)。
  • (blas, lapack)
    • 这是一个非常实际的课堂笔记。BLAS (Basic Linear Algebra Subprograms) 和 LAPACK (Linear Algebra Package) 是用于高性能科学计算（如矩阵对角化、求逆等）的黄金标准软件包。
    • 教授在这里的意思是：“这个矩阵运算（S^(-1/2)）我们手算不了，但计算机上的量子化学软件会调用 LAPACK 库来高效地完成它。”
  • F' C' = C' ε
    • 最终方程。重申上一张白板的结论：我们已经成功地将广义本征值问题 F C = S C ε 转换为了标准本征值问题 F' C' = C' ε。
    • 这是计算机可以（通过 LAPACK）直接求解的。
  • F' = S^(-1/2) F S^(-1/2) = (F')†
    • 这一行在确认一个重要的数学性质：F' 矩阵也是厄米 (Hermitian) 的。
    • † (dagger) 符号代表“厄米共轭”（转置并取复共轭）。
    • 因为 F 是厄米的 (F† = F)，S 也是厄米的，所以 F' 保证是厄米的。这确保了我们求解得到的轨道能量 ε 必定是实数，这在物理上是必需的。

Hartree-Fock (HF) 总能量

这是本张白板的核心。在 SCF 迭代收敛后，我们得到了所有的轨道能量 ε_i。那么，分子的总能量 E_HF 是多少？

一个常见的陷阱：你可能会认为总能量就是所有占据轨道的能量之和（2 Σ ε_i，因为每个轨道 2 个电子）。白板明确指出：这是错误的！

  • E_HF ≠ 2 Σ[i=1 to N/2] ε_i (总能量 ≠ 轨道能量之和)

    • 为什么？
    • 白板上的最后一行给出了答案。轨道能量 ε_i 的定义是： ε_i = <φ_i | f̂ | φ_i> = ε_ii + Σ[j=1 to N/2] (2J_ij - K_ij)
    • 物理含义：ε_i 不仅仅是电子 i 的能量，它代表了将一个电子加入到轨道 i 中所需要的能量。这个能量包括了：
      1. ε_ii：电子 i 自己的动能和它与所有原子核的吸引能。
      2. Σ[j] (2J_ij - K_ij)：电子 i 与所有其他 j 轨道电子的库仑排斥和交换作用。
    • 双重计算问题：
      • ε_i 包含了 i 与 j 的排斥能。
      • ε_j 包含了 j 与 i 的排斥能。
      • 如果你简单地将它们相加 (ε_i + ε_j)，你就把 i 和 j 之间的排斥能计算了两遍。
    • 因此，2 Σ ε_i 会双倍计算所有的电子-电子排斥能，导致结果错误。

  • 正确的 HF 总能量公式 白板给出了两个等价的正确公式：

    1. E_HF = 2 Σ[i] ε_ii + Σ[i,j] (2J_ij - K_ij) (白板第一行)
      • 2 Σ[i] ε_ii：所有电子的动能 + 电子-原子核吸引能（ε_ii 在这里是核心哈密顿积分 h_ii）。
      • Σ[i,j] (2J_ij - K_ij)：所有电子对之间的排斥/交换能（只计算一次！）。
    2. E_HF = Σ[i=1 to N/2] (ε_ii + ε_i) (白板中间行)
      • 这是一个更巧妙、更简洁的公式。
      • 它将总能量表示为：对所有占据轨道 i 求和，每一项是（核心哈密顿积分 ε_ii + 轨道能量 ε_i）。
      • 这个公式通过只加一次 ε_ii（单电子项）和一次 ε_i（包含单电子项和双电子项），巧妙地修正了双重计算问题，最终结果与公式 1 完全等价。

总结

从“如何求解”到“如何获取最终能量”的过渡。它展示了求解 F C = S C ε 的实用计算方法，并着重强调了 HF 总能量 E_HF 和轨道能量 ε_i 之间的关键区别。

IV

它用一个清晰的流程图 (Flowchart)，前面包含的所有复杂的数学公式和概念，总结成了一个完整的计算算法。

这就是 Hartree-Fock 自洽场 (Self-Consistent Field, SCF) 迭代循环的标准计算流程。

💡 SCF 流程图详解

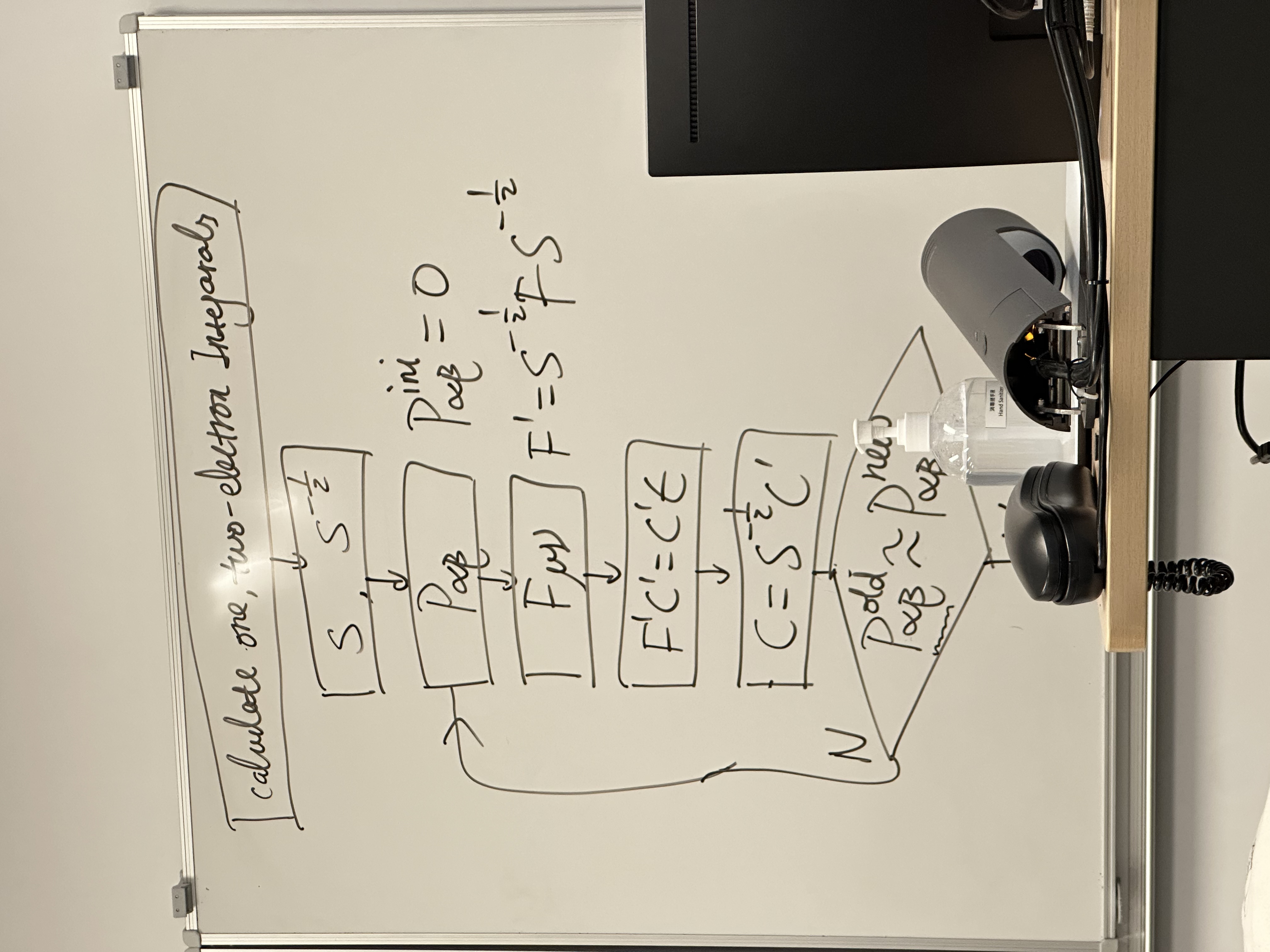
fusion

这个流程图展示了量子化学程序是如何一步步“猜”出正确答案的。

1. 准备工作 (循环开始前)

  • Calculate one, two-electron Integrals
    • 这是计算的“第 0 步”，在循环开始前只需要做一次。
    • 程序会计算所有需要的“积木块”：
      1. 单电子积分：重叠矩阵 S 和核心哈密顿矩阵 H_core。
      2. 双电子积分：所有 (μν|αβ) 形式的积分。这些积分数量极其庞大，是 HF 计算中最耗时的一步。
  • [ S -> S^(-1/2) ]
    • 利用第一步算出的 S 矩阵，计算出用于正交化的 S^(-1/2) 矩阵。这也只需要做一次。

2. SCF 迭代循环 (The Loop)

  • [ P_αβ ] (起始点)
    • 第 1 步：猜测。循环开始，我们必须提供一个初始的密度矩阵 P。
    • 白板上的 P_αβ^ini = 0 是一个最简单的“零猜测”，实际程序通常会用更高级的猜测方法（如 H_core 猜测）。
  • [ F_μν ]
    • 第 2 步：构建 Fock 矩阵。
    • 使用当前的密度矩阵 P_αβ，根据我们在第二张白板上的公式 F = H_core + G(P) 来构建当前的 Fock 矩阵 F。
  • [ F' C' = C' ε ]
    • 第 3 步：求解 Roothaan-Hall 方程。
    • 正如第三张白板所示，我们不直接解 F C = S C ε。
    • 我们先进行变换：F' = S^(-1/2) F S^(-1/2)。
    • 然后求解这个“标准本征值问题”，得到新的轨道能量 ε 和变换后的系数 C'。
  • [ C = S^(-1/2) C' ]
    • 第 4 步：反变换。
    • 用 S^(-1/2) 矩阵将 C' 转换回我们真正需要的、在原子轨道基组下的系数矩阵 C。
  • [ P_αβ^old ~ P_αβ^new ] (决策点)
    • 第 5 步：检查自洽性 (Convergence Check)。
    • 使用第 4 步得到的新 C，计算出一个新的密度矩阵 P^new。
    • 比较这个 P^new 和我们在第 2 步中使用的 P^old。
    • N (No)： 如果 P^new 和 P^old 差别很大（未收敛），则自洽尚未达成。
      • 循环：将 P^new 作为下一次迭代的 P，返回第 2 步（[ F_μν ]），用这个新的 P 去构建新的 F。
    • Y (Yes，未画出)： 如果 P^new 和 P^old 几乎完全相同（差值小于某个阈值，例如 10⁻⁸），则说明“自洽”达成！
      • 循环结束。

总结

以上内容从“为什么”（HF 近似）到“是什么”（HF 方程和矩阵）再到“怎么做”（SCF 流程图）。

SCF 流程是所有基于 Hartree-Fock 方法（以及更高级的后 HF 方法）的计算化学软件的核心算法。