PHYS 5120 - 计算能源材料和电子结构模拟 Lecture
I:
量子化学中的Hartree-Fock (HF) 理论。这是一个核心的近似方法,它将一个复杂的多电子问题简化为一组耦合的单电子问题。

1. N 电子波函数:Slater 行列式 (The \(N\)-electron Wavefunction: \(\Phi\))
- 概念: 对于一个 \(N\) 电子体系,其总波函数 \(\Phi\) 必须满足泡利不相容原理(Pauli Exclusion Principle),即交换任意两个电子的坐标(包括空间坐标 \(\vec{r}\) 和自旋坐标 \(\omega\)),波函数必须反号(反对称性)。
- Slater 行列式: 白板上指出 \(\Phi\) 是一个 Slater 行列式 (Slater determinant)。这是满足反对称性的最简单的波函数形式。它由 \(N\) 个单电子自旋-轨道 \(\phi_i\) 构筑而成。
- 公式: \[ \Phi(x_1, x_2,
\dots, x_N) = \frac{1}{\sqrt{N!}}
\begin{vmatrix}
\phi_1(x_1) & \phi_2(x_1) & \cdots & \phi_N(x_1) \\
\phi_1(x_2) & \phi_2(x_2) & \cdots & \phi_N(x_2) \\
\vdots & \vdots & \ddots & \vdots \\
\phi_1(x_N) & \phi_2(x_N) & \cdots & \phi_N(x_N)
\end{vmatrix}
\]
- \(x_i = (\vec{r}_i, \omega_i)\) 代表第 \(i\) 个电子的空间和自旋坐标。
- \(\frac{1}{\sqrt{N!}}\) 是归一化因子。
- 行列式的性质确保了:(1) 如果交换任意两行(交换两个电子),行列式变号。(2) 如果任意两个轨道相同(两列相同),行列式为零(即两个电子不能处于完全相同的状态)。
2. 自旋-轨道 (Spin-Orbitals: \(\phi_i\))
- 概念: 白板左侧定义了自旋-轨道 (spin-orbital),它是构成 Slater 行列式的基本单元。每个自旋-轨道 \(\phi_i\) 都是一个空间轨道 \(\psi_j\) 和一个自旋函数 \(\sigma\) 的乘积。
- 公式: \[\phi_i(x_i) =
\psi_j(\vec{r}_i) \sigma(\omega_i)\]
- \(\psi_j(\vec{r}_i)\) 是空间部分,如 \(1s\), \(2p_z\) 轨道,它描述了电子在空间中的分布。
- \(\sigma(\omega_i)\) 是自旋部分,只有两种可能:自旋向上 \(\alpha(\omega)\) (spin-up) 或自旋向下 \(\beta(\omega)\) (spin-down)。
3. Hartree-Fock 能量 (The Hartree-Fock Energy: \(E_{HF}\))
- 概念: 体系的总能量 \(E\) 是通过求解定态薛定谔方程 \(\hat{H}\Phi = E\Phi\) 得到的。在 HF 理论中,我们使用 Slater 行列式 \(\Phi\) 作为真实波函数的近似,并通过变分原理计算其能量期望值。这个能量就是 Hartree-Fock 能量 \(E_{HF}\)。
- 公式: \[E_{HF} =
\langle\Phi|\hat{H}|\Phi\rangle = \int \Phi^* \hat{H} \Phi
\,d\tau\]
- \(\hat{H}\) 是体系的总哈密顿算符(Hamiltonian operator),即总能量算符。
- \(\langle\Phi|...|\Phi\rangle\) 是 bra-ket 记号,代表对所有电子的所有坐标进行积分。
4. 能量的组成 (Components of the Energy)
- 概念: 将上述 \(\Phi\) 和 \(\hat{H}\)(包含所有电子的动能、核-电吸引、电-电排斥)代入 \(E_{HF}\) 的 积分并化简(这个过程被称为 Slater-Condon 规则),可以得到白板上最重要的核心公式:
- 公式 (1) - 总结形式: \[E_{HF} = \sum_{i=1}^{N} E_{ii} + \frac{1}{2}
\sum_{i,j=1}^{N} (J_{ij} - K_{ij})\]
- 这个公式将总能量分解为三部分。\(\frac{1}{2}\) 因子是为了在 \(i,j\) 双重求和中避免重复计算电子对(\(i,j\) 对和 \(j,i\) 对)。当 \(i=j\) 时,\(J_{ii} = K_{ii}\),所以 \(J_{ii} - K_{ii} = 0\),求和中可以包含 \(i=j\) 项。
下面我们来详细分解这三项:
A. 单电子能量 (\(E_{ii}\) 或 \(h_{ii}\))
- 概念: 这是第 \(i\) 个电子在自旋-轨道 \(\phi_i\) 上的核心能量。它包括该电子自身的动能和它与所有原子核之间的库仑吸引能。
- 公式: \[E_{ii} =
\langle\phi_i|\hat{h}|\phi_i\rangle = \int \phi_i^*(x_1) \left[
-\frac{\hbar^2}{2m}\nabla_1^2 + V_{\text{nuc}}(\vec{r}_1) \right]
\phi_i(x_1) \,dx_1\]
- \(\hat{h} = -\frac{\hbar^2}{2m}\nabla^2 + V_{\text{nuc}}(\vec{r})\) 是单电子核心哈密顿算符。
- \(V_{\text{nuc}}(\vec{r}_1)\) 是电子 1 与所有原子核之间的吸引势能(白板上写作 \(V_{\text{ext}}\),即外部势)。
B. 库仑积分 (Coulomb Integral: \(J_{ij}\))
- 概念: 这是经典的静电排斥能。它代表了处于 \(\phi_i\) 轨道的电子电荷云(密度为 \(|\phi_i|^2\))和处于 \(\phi_j\) 轨道的电子电荷云(密度为 \(|\phi_j|^2\))之间的平均静电排斥能。
- 公式: (如白板中间所推导) \[J_{ij} = \langle\phi_i \phi_j |
\frac{e^2}{|\vec{r}_1 - \vec{r}_2|} | \phi_i \phi_j \rangle = \iint
|\phi_i(x_1)|^2 \frac{e^2}{|\vec{r}_1 - \vec{r}_2|} |\phi_j(x_2)|^2
\,dx_1 dx_2\]
- \(J_{ij}\) 总是正值(\(J_{ij} > 0\)),它使体系的总能量升高(排斥作用)。
C. 交换积分 (Exchange Integral: \(K_{ij}\))
- 概念: 这是纯粹的量子力学效应,没有经典对应。它源于波函数的反对称性(泡利原理)。它只存在于自旋相同的电子对之间(白板上用 \(\delta(\sigma_i, \sigma_j)\) 或 \(\delta_{\sigma_i \sigma_j}\) 表示)。
- 公式: (如白板中间所推导) \[K_{ij} = \langle\phi_i \phi_j |
\frac{e^2}{|\vec{r}_1 - \vec{r}_2|} | \phi_j \phi_i \rangle = \iint
\phi_i^*(x_1) \phi_j^*(x_2) \frac{e^2}{|\vec{r}_1 - \vec{r}_2|}
\phi_j(x_1) \phi_i(x_2) \,dx_1 dx_2\]
- 关键区别: 注意 \(J_{ij}\) 和 \(K_{ij}\) 在积分号内右侧的区别。在 \(K_{ij}\) 中,电子 1 和 2 在末态轨道上 “交换” 了位置。
- \(K_{ij}\) 也是正值(\(K_{ij} > 0\))。但在总能量公式中,它以 \(-K_{ij}\) 出现。
- 物理意义: 这意味着交换作用使体系的总能量降低(体系更稳定)。
5. 洪德定则 (Hund’s Rule)
- 概念: 白板底部写着 “\(\uparrow\uparrow \downarrow\uparrow \uparrow\uparrow\) is the ‘#’ Hund’s rule” (\(\uparrow\uparrow\) 能量更低)。这正是交换积分 \(K_{ij}\) 的直接物理后果。
- 解释:
- 洪德第一定则:电子在填充简并轨道(能量相同的轨道)时,会优先自旋平行地(\(\uparrow\uparrow\))分占不同轨道,以使总自旋最大。
- 原因:
- 对于 \(\uparrow\uparrow\)(自旋平行)状态:两个电子自旋相同,它们之间的交换积分 \(K_{ij} \neq 0\)。总能量中包含 \(-K_{ij}\) 项,使能量降低。
- 对于 \(\uparrow\downarrow\)(自旋反平行)状态:两个电子自旋不同,它们之间的交换积分 \(K_{ij} = 0\)。没有交换作用带来的能量降低。
- 因此,自旋平行的 \(\uparrow\uparrow\) 状态能量更低、更稳定,这正是 \(K\) 项(交换能)导致的。
6. Hartree-Fock 方程 (The HF Equation)
- 概念: 白板最右侧开始写的 “HF eq…”。我们有了总能量 \(E_{HF}\) 的表达式,但我们还不知道 “最好” 的 \(\phi_i\) 是什么。HF 方法的目标就是找到一组 \(\phi_i\),使 \(E_{HF}\) 能量最低。
- 方法: 使用变分法,在保持轨道 \(\phi_i\) 归一正交的约束下,最小化 \(E_{HF}\)(即 \(\delta E_{HF} = 0\))。
- 结果: 这样做会得到一组 \(N\) 个耦合的单电子方程,即
Hartree-Fock 方程: \[\hat{f}(x_1) \phi_i(x_1) = \epsilon_i
\phi_i(x_1)\]
- \(\epsilon_i\) 是第 \(i\) 个自旋-轨道的轨道能 (orbital energy)。
- \(\hat{f}(x_1)\) 是Fock 算符 (Fock operator),它是一个等效的单电子哈密顿算符。
- Fock 算符 \(\hat{f}\): \[\hat{f}(x_1) = \hat{h}(x_1) + \sum_{j=1}^{N}
\left[ \hat{J}_j(x_1) - \hat{K}_j(x_1) \right]\]
- \(\hat{h}(x_1)\):就是之前的单电子核心算符(动能 + 核吸引)。
- \(\hat{J}_j(x_1)\):库仑算符,代表电子 1 受到 \(\phi_j\) 轨道上电子的平均静电排斥。
- \(\hat{K}_j(x_1)\):交换算符,代表电子 1 受到 \(\phi_j\) 轨道上电子的(仅当自旋相同时才有的)交换”吸引”。
- 自洽场 (Self-Consistent Field, SCF): HF
方程的”棘手”之处在于 \(\hat{f}\)
算符本身依赖于它要求解的 \(\phi_j\)
轨道。这必须通过迭代法求解,即 SCF 方法:
- 猜测一组 \(\phi_j\)。
- 用 \(\phi_j\) 构建 \(\hat{f}\) 算符。
- 求解 \(\hat{f}\phi_i = \epsilon_i \phi_i\) 得到一组新的 \(\phi_i\)。
- 重复 2-3 步,直到输入的 \(\phi_j\) 和输出的 \(\phi_i\) 不再变化(达到”自洽”)为止。
II
从左到右展示了 Hartree-Fock (HF) 方程的最终形式、如何将其简化为闭壳层 (closed-shell) 情况,以及最终如何通过 LCAO 近似 将其转化为可解的矩阵方程,即 Roothaan-Hall 方程。

1. Hartree-Fock (HF) 方程的推导与形式
白板的左侧展示了 HF 方程本身,它是通过变分法推导出来的。
- 变分法 (Variational Principle): \[\delta \left( \langle\Phi|\hat{H}|\Phi\rangle -
\sum_{i,j} \epsilon_{ij} (\langle\phi_i|\phi_j\rangle - \delta_{ij})
\right) = 0\]
- 这是一个约束下的最小化问题。我们要求总能量 \(E_{HF} = \langle\Phi|\hat{H}|\Phi\rangle\) 的变分(\(\delta\))为零(即找到能量最小值)。
- 约束条件是要求所有的自旋-轨道 \(\phi_i\) 必须保持归一正交(\(\langle\phi_i|\phi_j\rangle = \delta_{ij}\))。
- \(\epsilon_{ij}\) 是拉格朗日乘子 (Lagrange multipliers),在最终的方程中,对角项 \(\epsilon_{ii}\) 就被证明是轨道能 \(\epsilon_i\)。
- Hartree-Fock 方程 (HF equation):
对上述变分表达式求解,最终会得到 \(N\)
个耦合的单电子方程,白板上写出了其中第 \(i\) 个方程: \[\left[ -\frac{\hbar^2}{2m}\nabla_i^2 +
V_{\text{ext}}(\vec{r}_i) \right] \phi_i(\vec{r}_i) + \sum_{j} \left(
\dots \right) - \sum_{j} \left( \dots \right) = \epsilon_i
\phi_i(\vec{r}_i)\] 这个方程可以更紧凑地写为: \[\hat{f}(x_1) \phi_i(x_1) = \epsilon_i
\phi_i(x_1)\]
- \(\epsilon_i\) 是第 \(i\) 个自旋-轨道的轨道能。
- \(\hat{f}(x_1)\) 是Fock 算符 (Fock operator),它是一个等效的单电子哈密顿算符。
- SCF (自洽场): 如上一张图所述,Fock 算符 \(\hat{f}\) 本身又依赖于所有的 \(\phi_j\) 轨道。因此,这个方程必须通过自洽场 (Self-Consistent Field, SCF) 方法迭代求解。
2. 闭壳层 (Closed-Shell) 近似 (RHF)
白板右上方引入了一个重要的简化:闭壳层 (closed shell)。
- 概念: 假设体系中的 \(N\) 个电子(\(N\) 必须是偶数)两两配对,占据了 \(N/2\) 个空间轨道 \(\psi_i\)。每个空间轨道 \(\psi_i\) 都被一个自旋向上 (\(\alpha\)) 和一个自旋向下 (\(\beta\)) 的电子同时占据。
- 能量公式 (RHF Energy):
在这种情况下,总能量公式(如上一张图所示)可以被积分并简化,求和从 \(N\) 个自旋-轨道转变为 \(N/2\) 个空间轨道: \[E_{HF} = 2 \sum_{i=1}^{N/2} E_{ii} +
\sum_{i,j=1}^{N/2} (2J_{ij} - K_{ij})\]
- \(E_{ii} = \langle\psi_i|\hat{h}|\psi_i\rangle\),是空间轨道 \(\psi_i\) 的核心能。因子 2 是因为每个轨道有两个电子。
- \(J_{ij}\) 和 \(K_{ij}\) 现在是空间轨道 \(\psi_i\) 和 \(\psi_j\) 之间的库仑积分和交换积分。
- \(2J_{ij}\):代表 \(\psi_i\) 中的两个电子和 \(\psi_j\) 中的两个电子之间的所有 4 种库仑排斥。
- \(-K_{ij}\):代表 \(\psi_i\) 和 \(\psi_j\) 中自旋相同的电子对(\(\alpha\) 对 \(\alpha\), \(\beta\) 对 \(\beta\))之间的 2 种交换作用。
- Fock 算符 (RHF Fock Operator): \(\hat{f} |\phi_i \rangle = \epsilon_i |\phi_i
\rangle\) 这一行是 HF
方程的抽象形式。在闭壳层情况下,它被改写为空间轨道的方程: \[\hat{f}(\vec{r}_1) \psi_i(\vec{r}_1) = \epsilon_i
\psi_i(\vec{r}_1)\] 其中,闭壳层 Fock 算符 \(\hat{f}\) 定义为: \[\hat{f}(\vec{r}_1) = \hat{h}(\vec{r}_1) +
\sum_{j=1}^{N/2} [2\hat{J}_j(\vec{r}_1) - \hat{K}_j(\vec{r}_1)]\]
- \(\hat{h}\) 是单电子核心算符(动能+核吸引)。
- \(\hat{J}_j\) 和 \(\hat{K}_j\) 是根据空间轨道 \(\psi_j\) 定义的库仑算符和交换算符。
- 库仑和交换算符 (Coulomb and Exchange Operators):
白板中间定义了这两个算符如何作用在一个任意函数 \(\psi(\vec{r}_1)\) 上:
- 库仑算符 \(\hat{J}_j\): \[\hat{J}_j(\vec{r}_1) \psi_i(\vec{r}_1) = \left[ e^2 \int d\vec{r}_2 \frac{|\psi_j(\vec{r}_2)|^2}{|\vec{r}_1 - \vec{r}_2|} \right] \psi_i(\vec{r}_1)\] 它是一个局域 (local) 算符。它代表电子 1 受到 \(\psi_j\) 轨道中电子的平均电荷云 \(|\psi_j|^2\) 所产生的经典静电排斥势。
- 交换算符 \(\hat{K}_j\): \[\hat{K}_j(\vec{r}_1) \psi_i(\vec{r}_1) = \left[ e^2 \int d\vec{r}_2 \frac{\psi_j^*(\vec{r}_2) \psi_i(\vec{r}_2)}{|\vec{r}_1 - \vec{r}_2|} \right] \psi_j(\vec{r}_1)\] 它是一个非局域 (non-local) 算符。算符 \(\hat{K}_j\) 对 \(\psi_i\) 在 \(\vec{r}_1\) 处的作用,却依赖于 \(\psi_i\) 和 \(\psi_j\) 在所有其他点 \(\vec{r}_2\) 的值。这是 HF 理论的数学难点。
3. LCAO 近似与 Roothaan-Hall 方程
我们仍然无法直接解出 \(\psi_i\)。实际计算中,我们采用 LCAO (Linear Combination of Atomic Orbitals) 近似。
LCAO 近似: \[|\psi_i\rangle = \sum_{\mu=1}^{M} c_{\mu i} |\chi_\mu\rangle\]
- 我们将未知的分子轨道 \(\psi_i\) 展开为一组已知的基函数 (basis functions) \(\chi_\mu\) 的线性组合。
- 这组基函数通常是 centred 在每个原子上的原子轨道(如 1s, 2p 等),共 \(M\) 个。
- \(c_{\mu i}\) 是分子轨道系数。我们的问题从“求解一个复杂的函数 \(\psi_i\)”转变为“求解一组最佳的系数 \(c_{\mu i}\)”。
推导 Roothaan-Hall 方程: 我们将 LCAO 展开式代入 HF 方程 \(\hat{f} |\psi_i\rangle = \epsilon_i |\psi_i\rangle\): \[\hat{f} \sum_{\mu} c_{\mu i} |\chi_\mu\rangle = \epsilon_i \sum_{\mu} c_{\mu i} |\chi_\mu\rangle\] 然后,从左侧乘上另一个基函数 \(\langle\chi_\nu|\) 并对全空间积分: \[\sum_{\mu} c_{\mu i} \langle\chi_\nu|\hat{f}|\chi_\mu\rangle = \epsilon_i \sum_{\mu} c_{\mu i} \langle\chi_\nu|\chi_\mu\rangle\] 这在白板的右下角有清晰的展示。
Roothaan-Hall 方程 (矩阵形式): 我们可以将上式定义为矩阵元:
- Fock 矩阵 \(F\): \(F_{\nu\mu} = \langle\chi_\nu|\hat{f}|\chi_\mu\rangle\)
- Overlap 矩阵 \(S\): \(S_{\nu\mu} = \langle\chi_\nu|\chi_\mu\rangle\) (基函数 \(\chi\) 通常不是正交的,所以 \(S \neq I\))
- 系数矩阵 \(C\): \(C_{\mu i} = c_{\mu i}\)
- 轨道能矩阵 \(\epsilon\): \(\epsilon_{ij} = \epsilon_i \delta_{ij}\) (一个对角矩阵)
于是,上述方程 \(\sum_{\mu} F_{\nu\mu} C_{\mu i} = \sum_{\mu} S_{\nu\mu} C_{\mu i} \epsilon_i\) 就可以写成一个简洁的矩阵方程: \[\mathbf{F} \mathbf{C} = \mathbf{S} \mathbf{C} \mathbf{\epsilon}\] 这正是白板最底部所写的
( F ) ( C ) = ( S ) ( C ) ( ε )。 这是一个广义本征值问题 (generalized eigenvalue problem)。由于 Fock 矩阵 \(\mathbf{F}\) 依赖于系数矩阵 \(\mathbf{C}\)(因为 \(\hat{f}\) 依赖于 \(\psi_j\),而 \(\psi_j\) 依赖于 \(c_{\mu j}\)),这个方程仍然必须通过 SCF 迭代 求解,直到 \(C\) 和 \(\epsilon\) 不再变化为止。
III
这张白板继续深入推导,展示了如何将抽象的 Roothaan-Hall 方程 (\(\mathbf{F} \mathbf{C} = \mathbf{S} \mathbf{C} \mathbf{\epsilon}\)) 转化为在实际计算中可以求解的具体形式。
核心思想是:将 Fock 矩阵 \(F_{\mu\nu}\) 的每一个元素,分解为基于已知基函数 \(\chi\) 的积分。
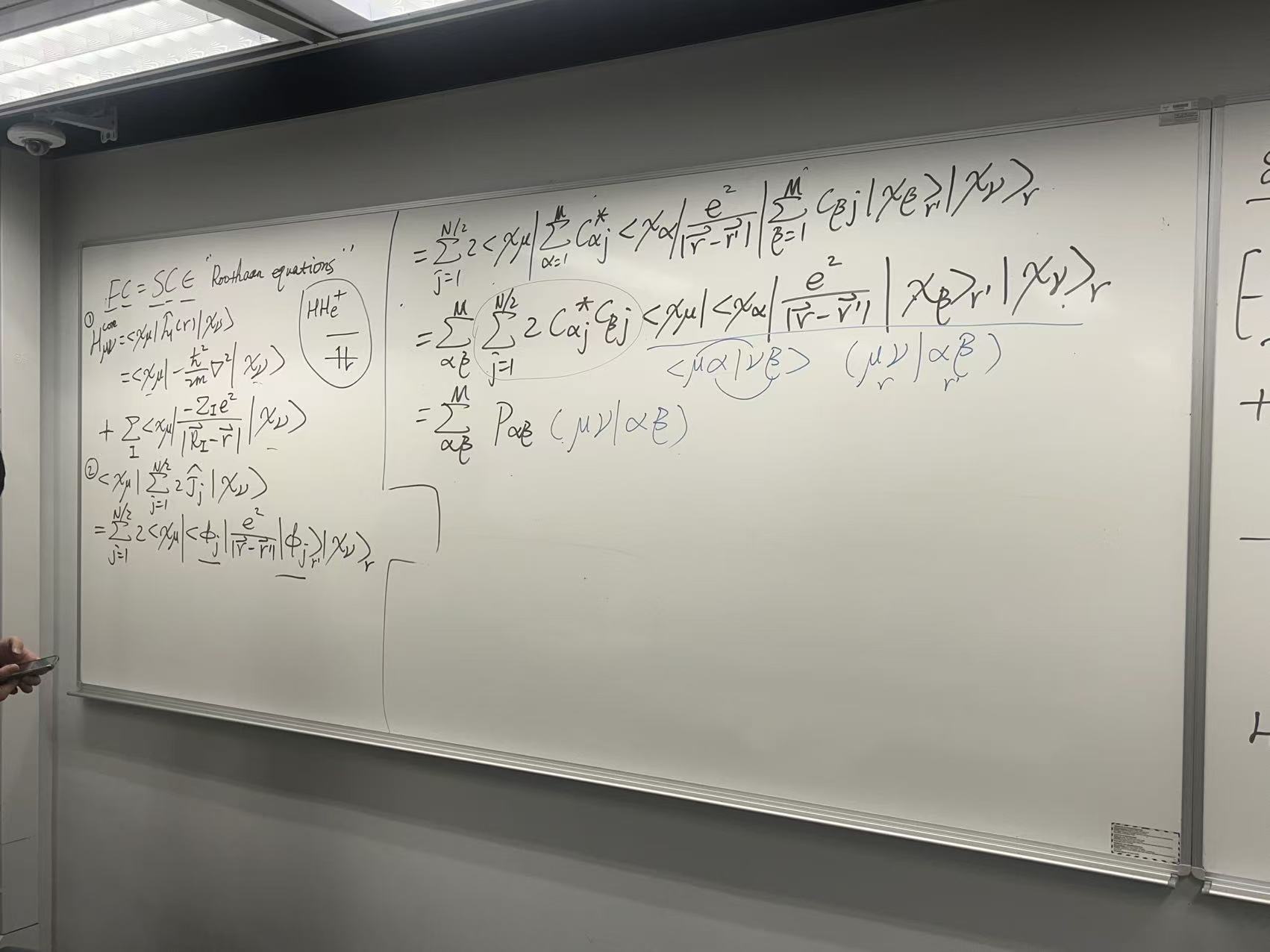
1. Fock 矩阵的构成 (Fock Matrix Elements)
白板左侧首先将 Fock 矩阵的元素 \(F_{\mu\nu}\) 分解为两部分:
\[F_{\mu\nu} = \langle\chi_\mu | \hat{f} | \chi_\nu\rangle = \langle\chi_\mu | \hat{h} + \sum_{j=1}^{N/2} (2\hat{J}_j - \hat{K}_j) | \chi_\nu\rangle\] \[F_{\mu\nu} = H_{\mu\nu}^{\text{core}} + G_{\mu\nu}\]
A. 核心哈密顿矩阵 (\(H_{\mu\nu}^{\text{core}}\))
- 概念: 这是单电子部分,代表一个电子在基函数 \(\chi_\mu\) 和 \(\chi_\nu\) 之间的”跳跃”能量。它只包含动能和与所有原子核的吸引能,不涉及电子间的排斥。
- 公式: \[H_{\mu\nu}^{\text{core}} = \langle\chi_\mu |
\hat{h} | \chi_\nu\rangle\] 其中,单电子核心哈密顿算符 \(\hat{h}\) 为: \[\hat{h} = -\frac{\hbar^2}{2m}\nabla^2 - \sum_A
\frac{Z_A e^2}{|\vec{r} - \vec{R}_A|}\]
- \(Z_A\) 和 \(\vec{R}_A\) 分别是原子核 A 的电荷和位置。
- 这一项在计算开始前就可以一次性计算并存储,因为它只取决于基函数和分子结构,不依赖于其他电子。
B. 双电子排斥矩阵 (\(G_{\mu\nu}\))
- 概念: 这是 \(F_{\mu\nu}\) 中最复杂的部分,包含了所有电子-电子之间的平均库仑排斥和交换作用。
- 公式: (对应白板左侧最下方的 @ 和 \(\Theta\) 项) \[G_{\mu\nu} = \sum_{j=1}^{N/2} \left( 2
\langle\chi_\mu | \hat{J}_j | \chi_\nu\rangle - \langle\chi_\mu |
\hat{K}_j | \chi_\nu\rangle \right)\]
- 这一项依赖于分子轨道 \(\psi_j\)(通过 \(\hat{J}_j\) 和 \(\hat{K}_j\)),而 \(\psi_j\) 正是我们要解的未知量。
2. 双电子积分 (Two-Electron Integrals, ERIs)
白板的右侧是整个推导的关键。它展示了如何通过代入 LCAO 近似(\(\psi_j = \sum_\alpha C_{\alpha j} \chi_\alpha\))来消除对未知 \(\psi_j\) 的依赖,将其全部转化为对已知基函数 \(\chi\) 的积分。
A. LCAO 展开
我们将 LCAO 展开式代入 \(G_{\mu\nu}\) 中的库仑项和交换项。这会产生一个四重循环,涉及四个基函数。
- 双电子积分 (ERI) 记号:
白板使用了物理学家记号 (physicist’s notation): \[\langle\mu\alpha|\hat{g}|\nu\beta\rangle =
\langle\chi_\mu \chi_\alpha | \frac{e^2}{|\vec{r}_1 - \vec{r}_2|} |
\chi_\nu \chi_\beta \rangle\] \[=
\iint \chi_\mu^*(\vec{r}_1) \chi_\alpha^*(\vec{r}_2)
\frac{e^2}{|\vec{r}_1 - \vec{r}_2|} \chi_\nu(\vec{r}_1)
\chi_\beta(\vec{r}_2) \,d\vec{r}_1 d\vec{r}_2\]
- \(\mu, \nu\) 对应电子 1 的基函数。
- \(\alpha, \beta\) 对应电子 2 的基函数。
B. 库仑项 (Coulomb Term)
- 推导: \[2
\sum_{j=1}^{N/2} \langle\chi_\mu | \hat{J}_j | \chi_\nu\rangle = 2
\sum_{j=1}^{N/2} \sum_{\alpha, \beta} C_{\alpha j}^* C_{\beta j}
\langle\mu\alpha|\hat{g}|\nu\beta\rangle\]
- 这对应白板右侧的第一个长公式。
- 它代表了 \(\chi_\mu \chi_\nu\) 电荷密度(电子1)和所有 \(\chi_\alpha \chi_\beta\) 电荷密度(电子2)之间的库仑排斥。
C. 交换项 (Exchange Term)
- 推导: \[-\sum_{j=1}^{N/2} \langle\chi_\mu | \hat{K}_j |
\chi_\nu\rangle = -\sum_{j=1}^{N/2} \sum_{\alpha, \beta} C_{\alpha j}^*
C_{\beta j} \langle\mu\alpha|\hat{g}|\beta\nu\rangle\]
- 这对应白板右侧的第二个长公式。
- 请注意索引的变化: 库仑项是 \(\langle\mu\alpha|\hat{g}|\nu\beta\rangle\),交换项是 \(\langle\mu\alpha|\hat{g}|\beta\nu\rangle\)。在交换项中,电子 1 和 2 的末态基函数被交换了 (\(\nu \leftrightarrow \beta\))。
3. 密度矩阵 (Density Matrix, \(P\))
最后,为了简化公式并明确其依赖关系,我们将与系数 \(C\) 和 \(j\) 相关的求和项组合起来,定义一个新矩阵:密度矩阵 (Density Matrix) \(P\)。
定义:(基于白板的推导) \[P_{\beta\alpha} = \sum_{j=1}^{N/2} C_{\alpha j}^* C_{\beta j}\] (注:标准的化学定义通常是 \(P_{\beta\alpha} = 2 \sum_{j=1}^{N/2} C_{\alpha j}^* C_{\beta j}\)。白板似乎将因子 2 留在了外面,但最终目的是一样的。)
\(G_{\mu\nu}\) 的最终形式: 将 \(P\) 代入,双电子排斥矩阵 \(G_{\mu\nu}\) 可以写为: \[G_{\mu\nu} = \sum_{\alpha, \beta} P_{\beta\alpha} \left[ 2 \langle\mu\alpha|\hat{g}|\nu\beta\rangle - \langle\mu\alpha|\hat{g}|\beta\nu\rangle \right]\]
总结:自洽循环 (SCF Loop)
白板上的推导最终表明,Fock 矩阵 \(F_{\mu\nu}\) 的完整表达式为:
\[F_{\mu\nu} = H_{\mu\nu}^{\text{core}} + \sum_{\alpha, \beta} P_{\beta\alpha} \left[ 2 \langle\mu\alpha|\hat{g}|\nu\beta\rangle - \langle\mu\alpha|\hat{g}|\beta\nu\rangle \right]\]
这完美地展示了 SCF (自洽场) 的核心: 1. \(\mathbf{F}\) 依赖于 \(\mathbf{P}\):要构建 Fock 矩阵 \(\mathbf{F}\),你必须知道密度矩阵 \(\mathbf{P}\)。 2. \(\mathbf{P}\) 依赖于 \(\mathbf{C}\):要构建密度矩阵 \(\mathbf{P}\),你必须知道轨道系数矩阵 \(\mathbf{C}\)(通过 \(P_{\beta\alpha} = \sum_j C_{\alpha j}^* C_{\beta j}\))。 3. \(\mathbf{C}\) 依赖于 \(\mathbf{F}\):要找到系数矩阵 \(\mathbf{C}\),你必须求解 Roothaan-Hall 方程 \(\mathbf{F} \mathbf{C} = \mathbf{S} \mathbf{C} \mathbf{\epsilon}\)。
这就形成了一个闭环,必须通过迭代求解: 猜测 \(\mathbf{C}^{(0)}\) \(\to\) 计算 \(\mathbf{P}^{(0)}\) \(\to\) 构建 \(\mathbf{F}^{(0)}\) \(\to\) 求解 \(\mathbf{F}^{(0)}\mathbf{C}^{(1)} = \mathbf{S}\mathbf{C}^{(1)}\mathbf{\epsilon}^{(1)}\) 得到新的 \(\mathbf{C}^{(1)}\) \(\to\) … 循环直到 \(\mathbf{C}\) 不再变化。