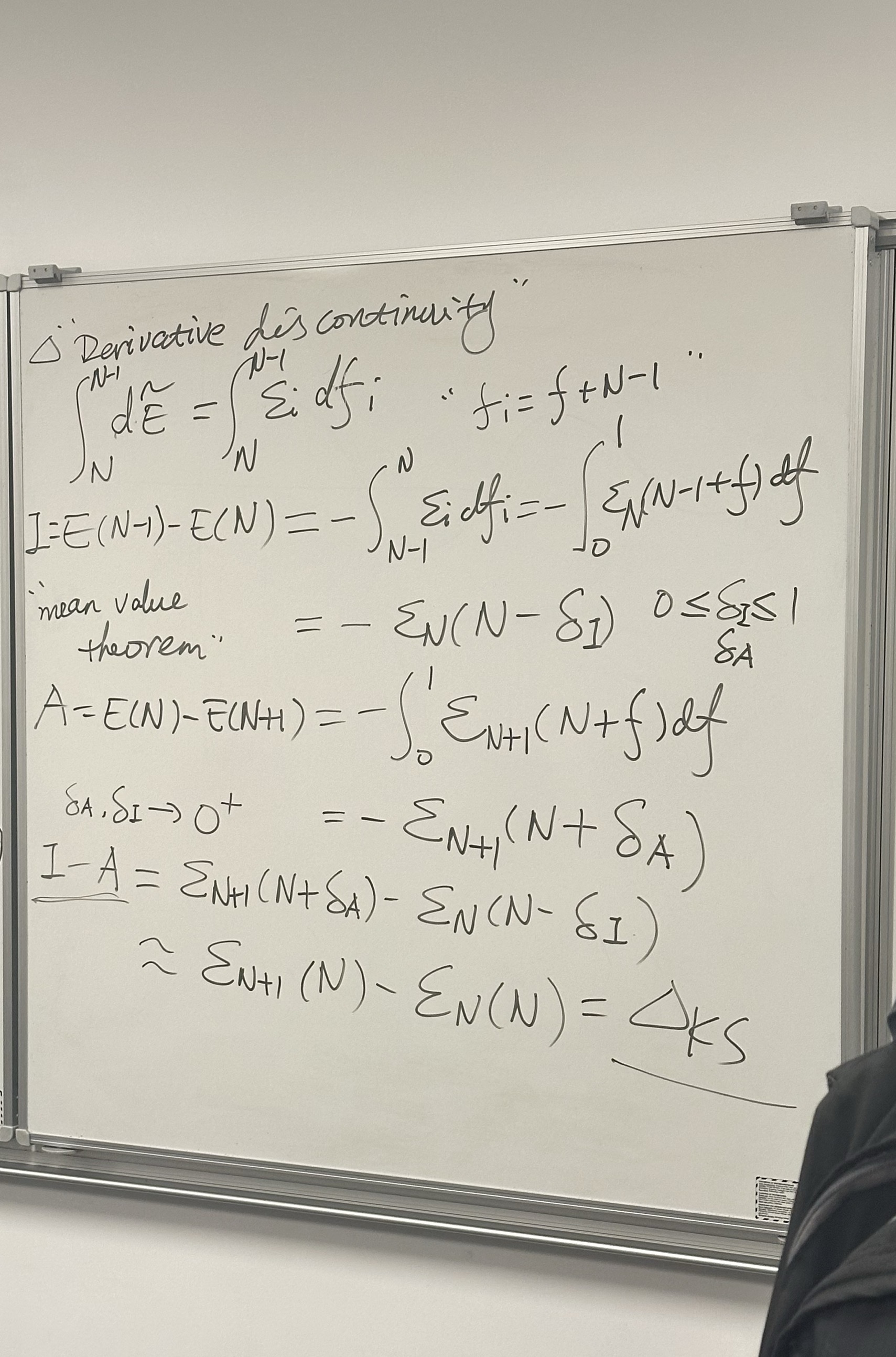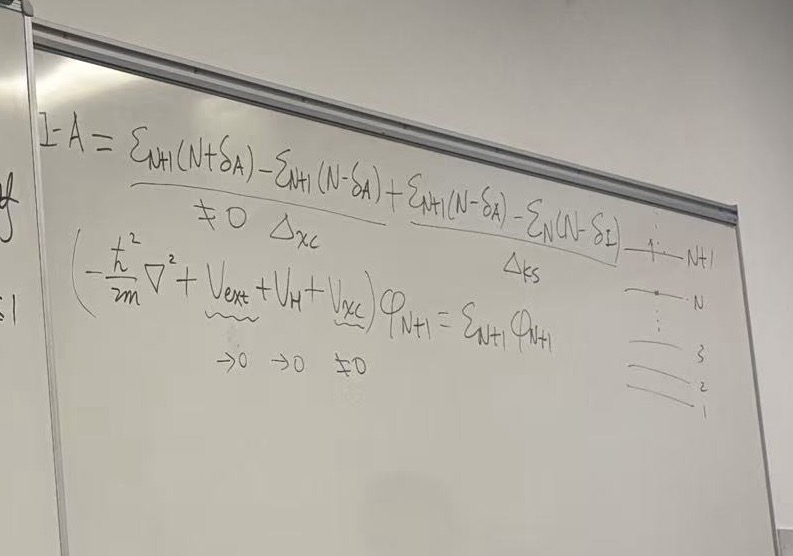PHYS 5120 - 计算能源材料和电子结构模拟 Lecture

Lecturer: Prof.PAN DING

Based on the image provided, these are notes from a physics lecture, specifically focusing on Density Functional Theory (DFT), Ensemble DFT, and the concept of Fractional Occupation.

The notes describe how to treat systems with a non-integer number of electrons to derive the “derivative discontinuity” of the energy, which is crucial for calculating band gaps (Ionization Potential minus Electron Affinity).

1. Center Panel: The Core Derivation (Ensemble DFT)

This section derives the energy of a system with a fractional number of electrons (\(N + \omega\)).

• Fractional Occupation: The total number of electrons is defined as an integer \(N\) plus a fraction \(\omega\). \[\int \rho(\vec{r}) \, d\vec{r} = N + \omega \quad \text{where } 0 \le \omega \le 1\]

• Density Operator (\(\hat{\rho}\)): The system is described as a mixed state (ensemble) of the \(N\)-particle state and the \((N+1)\)-particle state. \[\hat{\rho} = \alpha |\Psi_N\rangle\langle\Psi_N| + \beta |\Psi_{N+1}\rangle\langle\Psi_{N+1}|\]

  • Condition 1: Probabilities must sum to 1: \(\alpha + \beta = 1\).

• Energy Functional: The variational principle for the energy \(E[\rho]\) involves minimizing the trace of the density operator with the Hamiltonian (\(\hat{T} + \hat{V}_{ee}\)) plus the external potential term. \[E[\rho] = \min_{\hat{\rho} \to \rho(\vec{r})} Tr\left\{\hat{\rho}(\hat{T} + \hat{V}_{ee})\right\} + \int \rho(\vec{r}) V_{ext}(\vec{r}) \, d\vec{r}\]

• Electron Density: The density is the weighted sum of the densities of the two states. \[\rho(\vec{r}) = \langle \vec{r} | \hat{\rho} | \vec{r} \rangle = \alpha |\Psi_N|^2 + \beta |\Psi_{N+1}|^2\]

• Solving for Coefficients:

  • Using the particle number constraint: \(\alpha N + \beta(N+1) = N + \omega\).
  • Combining this with \(\alpha + \beta = 1\), the notes conclude: \[\alpha = 1 - \omega\] \[\beta = \omega\]

2. Left Panel: Citations & The Gap Question

This section lists key references discussing the “Derivative Discontinuity” and the fundamental gap (\(I - A\)).

• Heading: \(\Delta \mathcal{E}_i ?\) (Referring to the energy gap or derivative discontinuity).
• References:
  1. Dreizler & Gross: “ODFT: An Approach to the Quantum Many-Body Problem”.
  2. Perdew et al.: Phys. Rev. A 77, 012517 (2008); PNAS 114, 2801 (2017).
  3. Weitao Yang: J. Chem. Phys. 136, 204111 (2012).
• Key Equations:
  • Chemical potential/Orbital energy: \(\varepsilon_i = \frac{\partial E}{\partial f_i}\)
  • The Fundamental Gap (\(I - A\)): \[I - A = \mathcal{E}_{N+1}(N+\delta) - \mathcal{E}_{N}(N-\delta)\] (Note: The handwriting for the specific subscripts here is a bit quick, but it generally describes the difference in energy derivatives as \(\delta \to 0^+\), known as \(\Delta_{KS}\) or the Kohn-Sham gap correction).

3. Right Panel: Linearity Condition

Although partially cut off, this section outlines the famous PPLB (Perdew-Parr-Levy-Balduz) condition, which states that the energy of a fractional system should be linear between integers.

• The Equation: \[E(N+\omega) = (1-\omega)E(N) + \omega E(N+1)\]
• Derivatives: It shows the derivative of Energy (\(E\)) with respect to particle number (\(M\) or \(N\)) is constant between integers but jumps discontinuously at integer points.

Summary of Concepts

• Ensemble DFT: Standard DFT is for pure states. To describe fractional electrons, we use a statistical ensemble.
• Linearity: For the exact density functional, Energy vs. Particle Number is a series of straight line segments connecting integer points.
• The Gap: Because the slope changes at integers, the chemical potential jumps. This jump (derivative discontinuity) is essential for predicting accurate band gaps in solids, which standard approximations (like LDA/GGA) often fail to do.

This image is a direct continuation of the previous whiteboard. While the first board set up the Ensemble Density (mixing \(N\) and \(N+1\) states), this board uses that setup to prove the Linearity Condition of the energy and define the Chemical Potential.

1. Derivation of Energy Linearity (Top Section)

The board derives the famous result that for the exact functional, the energy varies linearly with fractional electron number.

• The Variational Principle: \[E[N+\omega] = \min_{\rho(\vec{r})} E[\rho]\]
• Expanding the Ensemble: Using the result from the previous board where \(\alpha = (1-\omega)\) and \(\beta = \omega\): \[= \min_{\rho} \left\{ (1-\omega)\langle\Psi_N|\hat{T}+\hat{V}_{ee}|\Psi_N\rangle + \omega\langle\Psi_{N+1}|\hat{T}+\hat{V}_{ee}|\Psi_{N+1}\rangle + \int \rho V_{ext} d\vec{r} \right\}\]
• Combining Terms: Since \(\hat{H} = \hat{T} + \hat{V}_{ee} + \hat{V}_{ext}\), the equation collapses into a weighted average of the energies of the integer states: \[= (1-\omega)\langle\Psi_N|\hat{H}|\Psi_N\rangle + \omega\langle\Psi_{N+1}|\hat{H}|\Psi_{N+1}\rangle\]
• The Boxed Result (The PPLB Condition): \[E(N+\omega) = (1-\omega)E(N) + \omega E(N+1)\] Significance: This proves that the ground state energy is a series of straight line segments connecting integer electron numbers. This is a fundamental constraint known as the Perdew-Parr-Levy-Balduz (PPLB) condition.

2. The Derivative Discontinuity (Middle & Graph)

The lecturer illustrates the consequence of the linearity derived above.

• The Graph:
  • The graph plots Energy (\(E\)) vs Electron Number (\(M\)).
  • The line connects \(E(N-1)\), \(E(N)\), and \(E(N+1)\).
  • Because the slope changes at \(N\), the derivative is discontinuous.
• Text Notation: \[\left. \frac{\partial E}{\partial M} \right|_{N \in I} \text{not continuous}\]
  • Slope to the left (\(N \to N-1\)): Related to Ionization Potential (\(I\)).
  • Slope to the right (\(N \to N+1\)): Related to Electron Affinity (\(A\)).

3. Chemical Potential and Variational Calculus (Bottom Section)

This section formally defines the chemical potential \(\mu\) using functional derivatives.

• Chain Rule for Total Derivative: \[\frac{\partial E}{\partial M} = \int \frac{\delta E[\rho]}{\delta \rho} \frac{\partial \rho}{\partial M} d\vec{r}\]
• Lagrange Multiplier Method: To minimize energy while keeping particle number \(M\) fixed, they introduce a Lagrange multiplier \(\lambda\): \[\frac{\delta \{E[\rho] - \lambda (\int \rho d\vec{r} - M) \}}{\delta \rho} = 0\]
• The Result: \[\frac{\delta E[\rho]}{\delta \rho} = \lambda = \mu\] This states that the functional derivative of the energy with respect to density is the chemical potential (\(\mu\)).

4. Right Panel (Partially Visible)

This side connects the formal theory to Kohn-Sham (KS) DFT.

• Diagram: Shows energy levels with occupied (solid lines) and unoccupied (dashed lines) orbitals.
• Equation: \(\Delta = I - A\). This defines the fundamental gap (band gap).
• Connection: In exact DFT, the chemical potential \(\mu\) jumps by an integer constant (the derivative discontinuity, \(\Delta_{xc}\)) when passing through an integer electron number. This “jump” is what’s missing in approximate functionals (like LDA/GGA), causing them to underestimate band gaps.

Summary of the Lecture: The professor is proving that if you treat a system with a fractional number of electrons correctly (as a statistical ensemble), the energy must result in straight lines between integers. Because of these straight lines, the slope (chemical potential) jumps at integers. This “Derivative Discontinuity” is the physical origin of the band gap in Density Functional Theory.

This third image serves as the conclusion of the derivation started in the previous two images. It connects the Fundamental Gap (experimental band gap) to the Kohn-Sham Gap (calculated band gap).

This is the mathematical proof of the “Band Gap Problem” in Density Functional Theory (DFT).

Here is the breakdown of the equations and logic on the board:

1. Left Panel: Defining the Gap via Chemical Potential

The board starts by defining the chemical potential (\(\mu\)) essentially as the slope of the energy curve derived in the previous images.

• Chemical Potential Limits: Depending on whether we are removing or adding an electron (approaching integer \(N\) from the left or right), the chemical potential \(\mu\) differs:

  • Electron Removal (\(M < N\)): \(\mu = -I\) (Ionization Potential).
  • Electron Addition (\(M > N\)): \(\mu = -A\) (Electron Affinity).

• The Fundamental Gap (\(\Delta_f\)): The fundamental gap is defined as the difference between the Ionization Potential and Electron Affinity: \[\Delta_f = I - A = \left. \frac{\delta E[\rho]}{\delta \rho} \right|_{N+\delta} - \left. \frac{\delta E[\rho]}{\delta \rho} \right|_{N-\delta}\] This represents the “jump” in the derivative of the total energy as you pass through the integer electron number \(N\).

• Total Energy Expansion: To find what causes this jump, the board writes out the standard Kohn-Sham total energy functional: \[E[\rho] = T_s[\rho] + \int V_{ext}\rho \, d\vec{r} + \frac{e^2}{2} \iint \frac{\rho \rho'}{|\vec{r}-\vec{r}'|} \, d\vec{r}d\vec{r}' + E_{xc}[\rho]\]

2. Right Panel: The Decomposition of the Gap

The goal here is to take the derivative of each term in the energy equation above and see which ones “jump” at integer \(N\).

\[\Delta_f = \left( \text{Difference in derivatives at } N+\delta \text{ and } N-\delta \right)\]

The board analyzes the terms one by one:

1. External Potential (\(V_{ext}\)): Continuous. No jump. (\(\rightarrow 0\))
2. Hartree/Coulomb Term (\(V_H\)): Continuous. No jump. (\(\rightarrow 0\))
3. Kinetic Energy Term (\(T_s\)): The derivative of kinetic energy with respect to density yields the Kohn-Sham eigenvalues (\(\varepsilon\)).
   • This difference is the Kohn-Sham Gap: \(\Delta_{KS} = \varepsilon_{LUMO} - \varepsilon_{HOMO}\).
4. Exchange-Correlation Term (\(V_{xc}\)):
   • \(\left. V_{xc} \right|_{N+\delta} - \left. V_{xc} \right|_{N-\delta} = C(N)\)
   • This term does not cancel. It is a constant shift in the potential known as the Derivative Discontinuity.

3. The Final Result (Boxed Equation)

At the bottom right, the lecture arrives at the critical conclusion:

\[\Delta_f = \Delta_{KS} + \Delta_{xc}\]

(Note: The board also labels \(\Delta_{xc}\) as \(C(N)\)).

What this means physically: * \(\Delta_f\): The real, physical band gap (measured experimentally as \(I - A\)). * \(\Delta_{KS}\): The band gap you calculate using the eigenvalues of the Kohn-Sham equations (\(\varepsilon_{N+1} - \varepsilon_N\)). * \(\Delta_{xc}\): The Derivative Discontinuity.

The Takeaway: The calculated Kohn-Sham gap (\(\Delta_{KS}\)) is NOT equal to the true fundamental gap (\(\Delta_f\)). It is missing a rigid shift constant, \(\Delta_{xc}\).

This explains why standard DFT (LDA/GGA) severely underestimates band gaps in semiconductors. Standard functionals “smooth out” the energy curve, effectively setting \(\Delta_{xc} \approx 0\), leaving you with only the \(\Delta_{KS}\), which is too small.

This fourth and final image connects the theoretical derivation from the previous boards to the practical reality of computational chemistry software. It explains why standard approximations fail and illustrates the algorithm used to solve these equations.

Here is the breakdown:

1. Left Panel: Why LDA & GGA Fail the Gap Test

This section explains why the “Band Gap Problem” exists in standard DFT calculations.

• The Failure of LDA/GGA: The notes state: \[\text{If LDA, GGA: } \quad V_{xc}[\rho] \bigg|_{N-\delta}^{N+\delta} \to 0\]
  • Meaning: In standard approximations like the Local Density Approximation (LDA) or Generalized Gradient Approximation (GGA), the exchange-correlation potential is a smooth, continuous function. It does not jump when the electron number crosses an integer.
  • Result: Because the “jump” (derivative discontinuity) is zero, the predicted band gap is just the Kohn-Sham gap (\(\Delta_{KS}\)), which we proved in the previous board is significantly smaller than the true fundamental gap. This is why standard DFT underestimates band gaps.
• The Theoretical Reason: > “\(E_{xc}[\rho]\) cannot be an explicit and differentiable functional of \(\rho\).”
  • For the “jump” to exist, the exact functional must have a “kink” at integer particle numbers. Smooth mathematical functions (like those used in LDA/GGA) cannot reproduce this kink.
• The Solution (Hybrid Functionals): The board lists: > “\(E_{xc}[\rho, \{\phi_i\}]\) PBE0, HSE06”
  • To fix the problem, we use functionals that depend on the orbitals (\(\phi_i\)) rather than just the density.
  • PBE0 & HSE06: These are “Hybrid Functionals” that mix in a portion of Exact Exchange (Hartree-Fock exchange). This orbital dependence reintroduces some of the derivative discontinuity, leading to much more accurate band gap predictions.

2. Right Panel: The Kohn-Sham SCF Loop

This flowchart illustrates the Self-Consistent Field (SCF) algorithm, which is the “engine” inside software like VASP, Gaussian, or Quantum ESPRESSO.

The Steps:

1. Initial Guess (\(\rho^{in}\)): The computer guesses an initial electron density \(\rho^{in}(\vec{r})\) (often a superposition of atomic densities).
2. Construct Hamiltonian (\(V_{KS}\)): Calculate the effective potential based on that guess: \[V_{KS} = V_{ext} + V_H[\rho^{in}] + V_{xc}[\rho^{in}]\]
3. Solve KS Equations: Solve the Schrödinger-like equation: \[\left( -\frac{1}{2}\nabla^2 + V_{KS} \right) \phi_i = \varepsilon_i \phi_i\]
4. Calculate New Density (\(\rho^{out}\)): Construct a new density from the orbitals you just found: \[\rho^{out} = \sum_i f_i |\phi_i(\vec{r})|^2\]
5. Check Convergence (Diamond Shape): Compare the new density (\(\rho^{out}\)) with the old one (\(\rho^{in}\)).
   • Is it Self-Consistent? (Is the difference roughly 0?)
     • NO: Update the guess by mixing the old and new densities to ensure stability (\(\alpha \rho^{out} + (1-\alpha)\rho^{in}\)) and go back to Step 2.
     • YES (OK): The calculation is finished. You have found the ground state.

Summary of the Whole Series

These four whiteboards tell a complete story of advanced DFT theory:

1. Board 1 & 2 (Ensemble Theory): We must treat fractional electron systems as statistical ensembles. This proves that Energy vs. Particle Number must be a series of straight lines (Linearity).
2. Board 2 & 3 (The Gap): Because of those straight lines, the slope (Chemical Potential) “jumps” at integers. This jump (\(\Delta_{xc}\)) is a crucial part of the real band gap.
3. Board 3 & 4 (The Problem & Solution): Standard DFT (LDA/GGA) misses this jump because it uses smooth functions, leading to wrong band gaps. To fix this, we use Hybrid Functionals (like HSE06) which depend on orbitals, and we solve them using the iterative SCF loop shown on the last board.

PHYS 5120 - 计算能源材料和电子结构模拟 Lecture

Lecturer: Prof.PAN DING

Based on the whiteboard image, these notes cover advanced topics in Density Functional Theory (DFT), specifically focusing on two major challenges: the treatment of Van der Waals (dispersion) forces and the physical interpretation of Kohn-Sham (KS) eigenstates (specifically the bandgap problem).

1. Left Panel: Van der Waals (vdW) Corrections

Standard DFT functionals (like LDA or GGA) often fail to describe long-range dispersion interactions (Van der Waals forces). The board lists three common strategies to correct this:

• Method 1: Semi-empirical Corrections (Grimme methods)
  • Notation: \(-\frac{C_6}{r^6}\)
  • Keywords: DFT-D2, DFT-D3, Grimme.
  • Explanation: This approach adds a simple pairwise semi-empirical potential term (based on the \(1/r^6\) decay) to the total energy to account for dispersion.
• Method 2: Tkatchenko-Scheffler (TS)
  • Citation: PRL 102, 073005 (2009)
  • Explanation: This refers to a method that derives dispersion coefficients (\(C_6\)) from the electron density itself, making it less empirical than standard Grimme corrections.
• Method 3: vdW-DF (Van der Waals Density Functional)
  • Citation: PRL 92, 246401 (2004)
  • Explanation: This refers to the Dion et al. functional, which includes a non-local correlation term to physically describe dispersion without empirical parameters.
• RPA (Random Phase Approximation): Listed at the bottom, this is a more computationally expensive method that naturally accounts for non-local electron correlation (including vdW) from first principles.

2. Middle Panel: KS Eigenstates & The Bandgap Problem

This section discusses the physical meaning of the eigenvalues obtained from the Kohn-Sham equations.

• The Kohn-Sham Equation: The board displays the fundamental equation for a single particle in an effective potential: \[\left(-\frac{\hbar^2}{2m}\nabla^2 + V_{KS}[\rho]\right) \phi_i = \epsilon_i \phi_i\]

• The “Bandgap Problem”:

  • Context: The notes mention “Koopmans’ theorem X”. In Hartree-Fock theory, Koopmans’ theorem links orbital energies to ionization energies. In DFT, this relationship is not straightforward for all orbitals.
  • The Issue: Standard DFT functionals typically underestimate the bandgap (the energy difference between the occupied and unoccupied states).

• Isolated Systems Limit: The notes explore the behavior of the wavefunction at the boundary:

  • Limit: \(\lim_{|\vec{r}|\to\infty} \psi = 0\) and \(V_{KS} = 0\)
  • Asymptotic behavior: \[-\frac{\hbar^2}{2m} \nabla^2 \phi_i = \epsilon_i \phi_i\] This describes the decay of the wavefunction far from the nucleus.

3. Right Panel (Partially Visible)

This section connects the Highest Occupied Molecular Orbital (HOMO) to physical observables.

• Asymptotic Decay: \(\phi_i = C e^{-\kappa r}\) (implied by the math). The decay rate of the density depends on the ionization potential.
• The Exact Condition: The text \(\epsilon_{HOMO} \to -I\) indicates a fundamental theorem in exact DFT: The energy of the highest occupied Kohn-Sham orbital is exactly equal to the negative of the ionization potential (\(I\)).
• \(\Delta\)SCF: This refers to the “Delta Self-Consistent Field” method, a way to calculate ionization energies or excitation energies by explicitly calculating the energy difference between the neutral and charged species (\(E_{N-1} - E_N\)), rather than relying solely on orbital eigenvalues.

Summary of References Cited

If you need to look up the specific papers mentioned on the left side of the board, here they are:

1. Tkatchenko & Scheffler: Phys. Rev. Lett. 102, 073005 (2009). “Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data.”

2. Dion et al. (vdW-DF): Phys. Rev. Lett. 92, 246401 (2004). “Van der Waals Density Functional for General Geometries.”

This image provides a deeper dive into the physical interpretation of Kohn-Sham eigenvalues, specifically contrasting how we treat finite systems (like molecules) versus infinite solids, and introducing the fundamental Janak’s Theorem.

Here is the breakdown of the notes, moving from left to right.

1. Left Panel: Finite Systems & The Meaning of \(\epsilon_{HOMO}\)

This section focuses on isolated systems (atoms/molecules) where the wavefunction decays to zero at infinity.

• Asymptotic Decay: The notes show the wavefunction \(\phi_i\) decaying exponentially as \(r \to \infty\): \[\phi_i \propto e^{-\sqrt{\frac{2m|\epsilon_i|}{\hbar^2}} r}\] This decay rate is determined physically by the Ionization Potential (\(I\)).

• The Exact DFT Condition: The box highlights a crucial theorem in exact DFT: \[\epsilon_{HOMO} = -I\] The eigenvalue of the Highest Occupied Molecular Orbital (HOMO) is physically meaningful—it equals the negative of the Ionization Potential. (Note: This is strictly true only for the exact functional, though approximate functionals often get the density right but the energy wrong).

• \(\Delta\)SCF Method: Since eigenvalues (\(\epsilon\)) in approximate DFT are often inaccurate, we use the Delta Self-Consistent Field (\(\Delta\)SCF) method to calculate gaps explicitly:

  • Ionization Potential (\(I'\)): \(E(N-1) - E(N)\)
  • Electron Affinity (\(A'\)): \(E(N) - E(N+1)\)
  • Fundamental Gap (\(\Delta_f\)): \(I - A\) This involves doing three separate calculations (neutral, cation, anion).

2. Right Panel: Solids & Janak’s Theorem

This is the most technically significant part of the board. It addresses the problem: How do we define these energies in a bulk solid where removing one electron from \(10^{23}\) atoms is negligible?

• The Problem with Solids: The notes state: In solid N ~ 10^23 -> infinity. It immediately notes Delta SCF X, meaning the \(\Delta\)SCF method is not practical or well-defined for calculating bandgaps in infinite periodic solids.

• Janak’s Theorem (1978):

  • Citation: Janak, Phys. Rev. B 18, 7165 (1978).
  • Concept: Janak generalized DFT to allow for fractional occupation numbers (\(f_i\)), where \(0 \le f_i \le 1\).
  • The Boxed Equation: \[\epsilon_i = \frac{\partial \tilde{E}}{\partial f_i}\] This is Janak’s Theorem. It states that the Kohn-Sham orbital energy \(\epsilon_i\) is the derivative of the total energy with respect to the occupation number of that orbital.

• Implication: This theorem connects the mathematical Lagrange multipliers (the eigenvalues \(\epsilon_i\)) to a physical derivative. It is the foundation for understanding why the “Bandgap Problem” exists.

  • In exact DFT, the energy \(E\) as a function of fractional electron number should be a series of straight lines (linearity condition).
  • Because standard functionals (LDA/GGA) are not linear (they are convex), the derivative \(\frac{\partial E}{\partial f_i}\) is incorrect at integer points, leading to the wrong bandgap.

• The Lemma/Proof (Bottom Right): The notes sketch the proof using the chain rule for functional derivatives: \[\frac{\partial F[\rho]}{\partial x} = \int \frac{\delta F[\rho]}{\delta \rho} \frac{\partial \rho}{\partial x} d\vec{r}\] This mathematical machinery is used to prove that the variation in energy comes from the variation in density caused by changing the occupation \(f_i\).

Summary of the Lesson

The board is teaching the derivation of the bandgap: 1. For Molecules: We can use \(\Delta\)SCF (calculating \(N\) and \(N \pm 1\) systems) to find the exact gap. 2. For Solids: We cannot use \(\Delta\)SCF. We must rely on the eigenvalues \(\epsilon_i\). 3. Janak’s Theorem proves that \(\epsilon_i\) is the derivative of the energy. 4. Therefore, if our energy functional has the wrong curvature (derivative) with respect to electron count (which LDA/GGA do), our bandgaps in solids will inevitably be wrong.

This concept is the “Holy Grail” for understanding why standard DFT fails to predict bandgaps correctly. It connects the math on the right side of your whiteboard (Janak’s Theorem) to the physical reality of electrons.

The explanation of Derivative Discontinuity and the Straight Line Condition.

1. The “Straight Line” Graph (Exact DFT)

Imagine a graph where the X-axis is the number of electrons (\(N\)) in a system, and the Y-axis is the Total Energy (\(E\)).

In the real world (and in exact DFT), electrons are discrete. You can have 1 electron or 2, but you cannot have 1.5 electrons on a single atom unless you treat it as a statistical ensemble (50% probability of having 1, 50% probability of having 2).

If you plot the energy for fractional electrons in exact DFT, the graph consists of straight line segments connecting the integer points.

• Slope to the left of integer \(N\): The energy cost to remove an electron. By definition, this slope is \(-I\) (Ionization Potential).
• Slope to the right of integer \(N\): The energy cost to add an electron. By definition, this slope is \(-A\) (Electron Affinity).

2. The “Discontinuity”

Here is the critical part: The slope changes abruptly at the integer.

The energy cost to remove an electron from a stable shell is high. The energy gain from adding an electron to a new, higher energy shell is low. Therefore, the slope on the left is steep, and the slope on the right is shallow.

• Janak’s Theorem (from your board) says: \(\epsilon = \frac{\partial E}{\partial f}\) (The eigenvalue is the slope).
• Because the slope changes, the eigenvalue \(\epsilon\) should jump as you cross the integer \(N\).
• This jump is called the Derivative Discontinuity (\(\Delta_{xc}\)).

The true fundamental gap (\(E_{gap}\)) is the difference between these two slopes: \[E_{gap} = I - A\]

3. The Problem with LDA/GGA (The “Convex” Curve)

Standard functionals like LDA or GGA violate this straight-line condition. Instead of a straight line, they produce a convex curve (like a hanging chain or a U-shape) between integers.

Because the curve is smooth and convex: 1. There is no jump in the slope at the integer \(N\). The slope just before \(N\) is almost the same as the slope just after \(N\). 2. This means the energy of the highest occupied state (\(\epsilon_{HOMO}\)) is predicted to be too high (too unstable), and the lowest unoccupied state (\(\epsilon_{LUMO}\)) is too low. 3. Result: The calculated bandgap is significantly smaller than the real bandgap.

4. Summary: The Equation

This leads to the famous decomposition of the bandgap.

In exact DFT, the true fundamental gap (\(E_{gap}\)) is the sum of the Kohn-Sham orbital gap (\(\epsilon_{gap}^{KS}\)) plus the discontinuity constant (\(\Delta_{xc}\)):

\[E_{gap} = \underbrace{(\epsilon_{LUMO} - \epsilon_{HOMO})}_{\text{DFT Bandgap}} + \underbrace{\Delta_{xc}}_{\text{Derivative Discontinuity}}\]

• In Exact DFT: \(\Delta_{xc}\) is large and positive. It accounts for the jump.
• In LDA/GGA: \(\Delta_{xc}\) is wrongly zero (or very close to it).
• Therefore: \(E_{gap} \approx \epsilon_{gap}^{KS}\). Since we are missing the positive \(\Delta_{xc}\) term, the DFT bandgap is underestimated (often by 30-50%).

How this connects to your whiteboard

On the right panel, the notes mention “In solid… \(\Delta\)SCF X”.

• For a molecule, you can manually calculate \(E(N)\) and \(E(N+1)\) to find the slopes (the \(\Delta\)SCF method).
• For a solid, you can’t easily add 1 electron to a bulk crystal. You have to rely on the eigenvalues (\(\epsilon\)).
• Since standard DFT (LDA/GGA) misses the Derivative Discontinuity, the eigenvalues \(\epsilon\) don’t reflect the true energy cost of adding/removing electrons, leading to the bandgap problem.

The mathematical proof of the “Derivative Discontinuity” concept we just discussed. It uses calculus to derive exactly why the standard DFT bandgap (\(\Delta_{KS}\)) is often an approximation that misses the real physics.

Here is the step-by-step breakdown of the derivation on the board:

1. Top Section: From Janak’s Theorem to Energy Differences

The derivation starts with Janak’s Theorem (\(\epsilon_i = \partial E / \partial f_i\)). To find the total energy difference between integer electron counts (like \(N\) and \(N-1\)), we must integrate this derivative.

• Equation: \(\int_N^{N-1} d\tilde{E} = \int_N^{N-1} \epsilon_i df_i\)
• Translation: The energy change when removing an electron is the sum (integral) of the orbital energy values as you slowly drain the electron density from \(1.0\) down to \(0.0\).

2. Middle Section: Defining Ionization (\(I\)) and Affinity (\(A\))

The board uses the Mean Value Theorem for integrals. This theorem states that \(\int_a^b g(x)dx = (b-a)g(c)\) for some point \(c\) in the interval.

• For Ionization Potential (\(I\)): \[I = E(N-1) - E(N)\] Using the Mean Value Theorem, this integral is equal to the eigenvalue \(\epsilon_N\) evaluated at some fractional electron count \(N - \delta_I\) (where \(0 \le \delta_I \le 1\)). \[I = -\epsilon_N(N-\delta_I)\]

• For Electron Affinity (\(A\)): \[A = E(N) - E(N+1)\] Similarly, this equals the eigenvalue of the next orbital (\(\epsilon_{N+1}\)) evaluated at a fractional count \(N+\delta_A\). \[A = -\epsilon_{N+1}(N+\delta_A)\]

3. Bottom Section: The Gap and the Approximation

This is the most important part. It combines \(I\) and \(A\) to find the Fundamental Gap (\(I - A\)).

• The Exact Gap: \[I - A = \epsilon_{N+1}(N+\delta_A) - \epsilon_N(N-\delta_I)\] This equation says the true gap depends on the eigenvalues at fractional occupations slightly away from the neutral state.

• The Approximation (The “Kohn-Sham Gap”): The last line shows what happens in standard DFT (LDA/GGA): \[\approx \epsilon_{N+1}(N) - \epsilon_N(N) = \Delta_{KS}\]

  Why is this an approximation? This step assumes that the eigenvalues \(\epsilon\) do not change significantly as you change the occupation numbers (\(\delta \to 0\)).

  • If there is no derivative discontinuity (like in LDA/GGA), the eigenvalues are continuous, so \(\epsilon(N+\delta) \approx \epsilon(N)\).
  • Therefore, you get the standard result: The Gap = LUMO energy - HOMO energy.

This board proves that \(\Delta_{KS}\) (the orbital gap) is only equal to the Fundamental Gap (\(I-A\)) if the derivative discontinuity is zero.

Since we know from exact quantum mechanics that the discontinuity is NOT zero (the slope must jump at integers), this derivation proves mathematically why standard DFT functionals (which lack this jump) are theoretically guaranteed to underestimate the bandgap.

This whiteboard contains the detailed mathematical derivation (proof) of Janak’s Theorem, which was introduced on the previous board.

Recall the theorem’s statement: \(\frac{\partial E}{\partial f_i} = \epsilon_i\). (The derivative of the total energy with respect to the occupation number of an orbital is equal to that orbital’s eigenvalue).

Here is the line-by-line breakdown of the proof shown on the board:

1. The Goal

The derivation starts at the top left: \[\frac{\partial \tilde{E}}{\partial f_i} = \dots\] We are calculating how the total energy changes when we add a tiny fraction of an electron to orbital \(i\).

2. Term-by-Term Differentiation

The total energy in DFT is a sum of Kinetic, External, Hartree, and Exchange-Correlation energies. The derivation differentiates each part separately:

• Kinetic Energy Term (Top Line): \[\langle \phi_i | -\frac{\hbar^2}{2m} \nabla^2 | \phi_i \rangle\] This is the expectation value of the kinetic energy for orbital \(i\).

• External Potential Term (2nd Line): \[+ \int V_{ext}(\vec{r}) |\phi_i(\vec{r})|^2 d\vec{r}\] Since the density \(\rho = \sum f_i |\phi_i|^2\), the derivative \(\frac{\partial \rho}{\partial f_i}\) is simply \(|\phi_i|^2\). This term represents the interaction of the specific orbital \(i\) with the nuclei.

• Hartree Term (3rd Line): \[+ \int d\vec{r} V_{Hartree}(\vec{r}) |\phi_i(\vec{r})|^2\] The derivative of the total Hartree energy with respect to density gives the Hartree Potential (\(V_{Hartree}\)).

• Exchange-Correlation Term (4th Line): \[+ \int d\vec{r} V_{xc}[\rho] |\phi_i(\vec{r})|^2\] Similarly, the derivative of the XC energy gives the XC Potential (\(V_{xc}\)).

3. Recombining the Terms

The lecturer then groups all these terms together into a single expectation value bracket:

\[= \langle \phi_i | -\frac{\hbar^2}{2m} \nabla^2 + \underbrace{V_{ext}(\vec{r}) + V_{Hartree}(\vec{r}) + V_{xc}(\vec{r})}_{V_{KS}(\vec{r})} | \phi_i \rangle\]

• The sum of the three potentials (External + Hartree + XC) is exactly the definition of the Kohn-Sham Effective Potential (\(V_{KS}\)).
• Therefore, the operator inside the bracket is the Kohn-Sham Hamiltonian (\(H_{KS}\)).

4. The Conclusion (Q.E.D.)

The final step relies on the Kohn-Sham equation itself (\(H_{KS} \phi_i = \epsilon_i \phi_i\)):

\[= \epsilon_i \quad \square\]

The expectation value of the Hamiltonian for an eigenvector is simply the eigenvalue. The square box (\(\square\)) is the symbol for “Q.E.D.” (quod erat demonstrandum), indicating the proof is complete.

Why this matters in the context of the lecture?

This proof solidifies the previous discussion about the bandgap. It mathematically proves that the eigenvalue \(\epsilon_i\) really is the energy cost of adding a fractional electron.

If the functional (like LDA/GGA) gets the energy curvature wrong (no derivative discontinuity), this derivative \(\epsilon_i\) will yield the wrong value for the gap, as shown in the previous slides.

This final whiteboard image brings the entire derivation to its “grand conclusion.” It combines the definitions of Ionization Potential (\(I\)) and Electron Affinity (\(A\)) to show exactly why standard DFT gets the bandgap wrong and what the missing piece is.

Here is the breakdown of the derivation on the board:

1. The “Magic” Decomposition (Top Equation)

The lecturer takes the definition of the fundamental gap (\(I - A\)) derived in the previous slide and performs a clever algebraic split by adding and subtracting the term \(\epsilon_{N+1}(N-\delta)\) (essentially the LUMO energy of the neutral system).

\[I - A = \underbrace{\epsilon_{N+1}(N+\delta_A) - \epsilon_{N+1}(N-\delta_A)}_{\Delta_{xc}} + \underbrace{\epsilon_{N+1}(N-\delta_A) - \epsilon_{N}(N-\delta_I)}_{\Delta_{KS}}\]

This splits the true bandgap into two distinct physical components:

• \(\Delta_{KS}\) (The Kohn-Sham Gap): This is the standard gap you get from a DFT output: LUMO energy minus HOMO energy.
  • \(\Delta_{KS} = \epsilon_{N+1}(N) - \epsilon_{N}(N)\)
• \(\Delta_{xc}\) (The Derivative Discontinuity): This is the “missing piece.” It represents how much the eigenvalue \(\epsilon_{N+1}\) jumps when you cross the integer electron count \(N\).
  • Mathematically: \(\lim_{\delta \to 0} [\epsilon_{N+1}(N+\delta) - \epsilon_{N+1}(N-\delta)]\)
  • The board notes: \(\neq 0\) (This term is not zero in exact theory).

2. The “Culprit” in the Hamiltonian (Middle Equation)

The board asks: Where does this discontinuity come from?

It writes out the Kohn-Sham equation for the \((N+1)\)-th electron: \[\left(-\frac{\hbar^2}{2m}\nabla^2 + V_{ext} + V_H + V_{xc}\right) \phi_{N+1} = \epsilon_{N+1} \phi_{N+1}\]

Underneath the potential terms, there are small arrows indicating whether these potentials experience a “jump” (discontinuity) when the electron count changes infinitesimally:

• \(V_{ext}\) (External Potential): \(\to 0\). The nuclear potential is fixed; it doesn’t care about electron count. It is continuous.
• \(V_{H}\) (Hartree Potential): \(\to 0\). The classical electrostatic potential is continuous with respect to small density changes.
• \(V_{xc}\) (Exchange-Correlation Potential): \(\neq 0\).
  • This is the key insight: The Exchange-Correlation potential jumps by a constant constant value everywhere in space the moment you add a fraction of an electron past integer \(N\).

3. The Final Conclusion

The fundamental gap is the sum of the calculated gap and this potential jump:

\[E_{gap}^{fund} = \Delta_{KS} + \Delta_{xc}\]

• In Standard DFT (LDA/GGA): The functional is smooth. It has no derivative discontinuity (\(\Delta_{xc} \approx 0\)). Therefore, \(E_{gap} \approx \Delta_{KS}\). This is why standard DFT underestimates the bandgap—it is missing the \(\Delta_{xc}\) term entirely.
• In Exact DFT: The potential \(V_{xc}\) jumps, providing the necessary energy correction to match the experimental gap (\(I-A\)).

Summary of the Full Lecture Sequence

Based on your four images, here is the complete narrative of the lecture:

1. The Problem: Standard DFT fails at Van der Waals forces and Bandgaps.
2. The Tool: Janak’s Theorem connects eigenvalues (\(\epsilon\)) to the derivative of energy (\(\partial E / \partial f\)).
3. The Proof: Using calculus, we proved Janak’s theorem and showed that the true gap depends on the slopes of the energy curve.
4. The Verdict (This Slide): The true gap (\(I-A\)) equals the DFT orbital gap (\(\Delta_{KS}\)) PLUS a derivative discontinuity (\(\Delta_{xc}\)). Standard functionals miss this discontinuity, which is why they fail for solids/semiconductors.

Uni-Mol2训练数据集详细参数表

Uni-Mol2相关数据集及资源链接汇总表

一、预训练数据集相关

二、下游任务数据集（QM9及衍生）

三、Uni-Mol Docking V2 相关（衍生任务）

四、论文及核心参考

PHYS 5120 - 计算能源材料和电子结构模拟 Lecture

Lecturer: Prof.PAN DING

在前面，我们看到了“理想”的无轨道 DFT (OF-DFT)，它试图将能量 \(E\) 直接写成密度 \(\rho\) 的泛函 \(E[\rho]\)。但它失败了，因为我们无法找到一个足够精确的动能泛函 \(T[\rho]\)。

接下来介绍的是Kohn-Sham (KS) DFT，它采用了一种“妥协”方案，彻底绕开了这个难题。

1. 概念回顾：无轨道 DFT 的困境

首先回顾我们已知的（也是 OF-DFT 的）总能量泛函：

\[E[\rho] = \underbrace{T[\rho]}_{\text{① 动能}} + \int V_{ext}(\vec{r})\rho(\vec{r})d\vec{r} + \underbrace{\frac{e^2}{2}\iint d\vec{r}d\vec{r}' \frac{\rho(\vec{r})\rho(\vec{r}')}{|\vec{r}-\vec{r}'|}}_{\text{Hartree 能量}} + \underbrace{E_{xc}[\rho]}_{\text{② 交换关联能}}\]

• 问题所在：
  • ① \(T[\rho]\) (动能)： 这是最大的难题。动能是一个与波函数曲率 (curvature) 相关的量子力学量 (\(\hat{T} \propto \nabla^2\))。我们无法简单地通过密度 \(\rho\)（一个标量场）来精确描述它。前面推导的 \(T[\rho] \propto \int \rho^{5/3} d\vec{r}\) 只是一个非常粗糙的近似。
  • ② \(E_{xc}[\rho]\) (交换关联能)： 这是第二个难题。它包含了所有复杂的、非经典的电子-电子相互作用（泡利不相容原理的交换效应、电子相互躲避的关联效应）。

KS-DFT 的目标就是同时解决这两个问题。

2. 核心概念：Kohn-Sham 辅助系统

Kohn-Sham 的核心思想是：“我承认 \(T[\rho]\) 太难了，所以我干脆不去近似它。”

Kohn-Sham 的核心假设： 对于任何一个我们关心的、有相互作用的真实系统（其基态密度为 \(\rho_{true}\)），我们总能构建一个虚构的 (fictitious)、无相互作用的辅助系统，这个系统被设计为恰好具有与真实系统完全相同的基态密度 \(\rho(\vec{r}) = \rho_{true}(\vec{r})\)。

这个想法彻底改变了规则。

• 公式 1：Kohn-Sham 哈密顿量 \(\hat{H}_{KS}\)
  • Ĥ_KS = -ħ²/2m ∇² + V_KS(r)
  • 这是一个描述 \(N\) 个无相互作用电子的哈密顿量，它们都在一个共同的有效势 \(V_{KS}(\vec{r})\) 中运动。
  • 关键点： 这个哈密顿量中没有电子-电子相互作用项（如 \(e^2/|\vec{r}_i - \vec{r}_j|\)）。这使得它在数学上变得极其简单。
• 公式 2：Kohn-Sham 波函数 \(\Phi\)
  • 一个斯莱特行列式：Φ = 1/√N! | ... |
  • 详细解释： 由于 \(\hat{H}_{KS}\) 是 \(N\) 个无相互作用粒子的哈密顿量（\(\hat{H}_{KS} = \sum_i \hat{h}_i\)），它的基态波函数 \(\Phi\) 可以被精确地写成一个由 \(N\) 个最低能量的单电子Kohn-Sham 轨道 \(\phi_i\) 构成的斯莱特行列式 (Slater Determinant)。
  • 这些轨道 \(\phi_i\) 是单粒子薛定谔方程（即 Kohn-Sham 方程）的解： \[\left( -\frac{\hbar^2}{2m}\nabla^2 + V_{KS}(\vec{r}) \right) \phi_i(\vec{r}) = \epsilon_i \phi_i(\vec{r})\]

3. 关键公式：密度和动能

现在，我们来看看这个“虚构系统”是如何帮我们解决问题的。

• 公式 3：KS 系统的电子密度 \(\rho(\vec{r})\)
  • ρ(r) = ⟨Φ| Σ δ(r-ri) |Φ⟩ = Σ_{i=1}^N |φ_i|²
  • 详细解释：
    • ⟨Φ| Σ δ(r-ri) |Φ⟩：这是密度 \(\rho(\vec{r})\) 的标准量子力学定义，即“在 \(\vec{r}\) 处找到任意一个电子的概率”。
    • = Σ_{i=1}^N |φ_i|²：这是最关键的简化。对于一个斯莱特行列式波函数 \(\Phi\)，总的电子密度精确地等于所有被占据的 KS 轨道的概率密度之和。
  • KS 假设的重申： 我们假设存在一个 \(V_{KS}(\vec{r})\)，使得这个 \(\rho(\vec{r})\) 恒等于我们想研究的真实系统的密度 \(\rho_{true}(\vec{r})\)。
• 公式 4：无相互作用动能 \(T_s[\rho]\)
  • Ts[ρ] = ⟨Φ| Σ -ħ²/2m ∇_i² |Φ⟩ = Σ_{i=1}^N ⟨φ_i| -ħ²/2m ∇² |φ_i⟩
  • 详细解释：
    • 这就是 KS 方案的全部意义！
    • 我们想知道这个虚构系统的总动能 \(T_s\) (s 代表 ‘single-particle’ 或 ‘non-interacting’)。
    • \(T_s = \langle \Phi | \hat{T} | \Phi \rangle\)。
    • 与密度一样，由于 \(\Phi\) 是斯莱特行列式，\(\hat{T}\) 是单体算符，总动能精确地等于所有被占据的 KS 轨道的动能之和。
  • 结论： 我们成功地避免了对 \(T[\rho]\) 的近似。我们现在不去近似它，而是通过求解 KS 轨道 \(\phi_i\) 来精确计算动能的主要部分 \(T_s\)。

4. “证明”：\(T_s[\rho]\) 与 \(T_{true}[\rho]\) 的关系

提出了一个问题和一个潦草的证明：

• 问题： Ts[ρ] ≤ T_true[ρ] ?

  • 我们通过轨道计算的无相互作用动能 \(T_s\) 与真实系统的真正动能 \(T_{true}\) 相比，哪个更大？

• 答案：\(T_s[\rho] \le T_{true}[\rho]\) 恒成立。

• 证明：

  • Proof: ⟨Φ_ks| ... 这里的字迹非常潦草，似乎是想用变分原理来论证，但写得并不清楚。

• 一个更清晰的、概念性的证明：

  1. \(T_s[\rho]\) 是一个无相互作用系统在密度为 \(\rho\) 时的基态动能。
  2. \(T_{true}[\rho]\) 是一个有相互作用系统在密度为 \(\rho\) 时的基态动能。
  3. 在真实系统中，电子不仅受 \(V_{ext}\) 束缚，它们还必须相互排斥 (correlation)。为了“躲避”彼此，它们的波函数必须变得更加“弯曲”或“扭动”。
  4. 在量子力学中，动能 \(\propto \int |\nabla \Psi|^2\)，它衡量的是波函数的“弯曲程度”。
  5. 真实电子为了相互躲避而增加的额外“弯曲”，导致了额外的动能。
  6. 因此，对于同一个密度 \(\rho\)，真实系统的动能 \(T_{true}\) 必然大于或等于那个不需要考虑相互躲避的、虚构的无相互作用系统的动能 \(T_s\)。

• 这引出了最终的 KS-DFT 能量划分：

  1. 真实动能 \(T_{true}\) 被拆分为：\(T_{true}[\rho] = T_s[\rho] + T_c[\rho]\)

     • \(T_s[\rho]\)：无相互作用动能（我们用轨道精确计算）。
     • \(T_c[\rho]\)：动能的关联部分（\(T_{true} - T_s\)，这是个未知的小量）。

  2. 现在，Kohn-Sham 方案将所有未知项——\(T_c[\rho]\) 和 \(E_{xc}[\rho]\)（来自 OF-DFT）—— 全部打包 进一个新的交换关联泛函 \(E_{xc}^{KS}[\rho]\) 中。

  3. Kohn-Sham 总能量泛函： \[E[\rho] = \mathbf{T_s[\{\phi_i\}]} + \int V_{ext}(\vec{r})\rho(\vec{r})d\vec{r} + E_H[\rho] + \mathbf{E_{xc}^{KS}[\rho]}\]

总结： KS-DFT 的赌注是：通过轨道精确计算 \(T_s\)，剩下的那个包含 \(T_c\) 的新 \(E_{xc}^{KS}[\rho]\)，会比原来那个包含整个 \(T_{true}\) 的 OF-DFT 泛函容易得多。

历史证明，这个赌注赢了。

现代 DFT 计算的核心——Kohn-Sham 方程。

它回答了两个终极问题： 1. 我们把所有“脏活累活”都塞进 \(E_{xc}\) (交换关联能) 里，那这个 \(E_{xc}\) 到底是什么？ 2. 我们如何求解这个 KS 系统来找到轨道 \(\phi_i\) 和密度 \(\rho\)？

1. 概念：\(E_{xc}\) 的正式定义 (左侧)

接下来给出了 Kohn-Sham 交换关联能 \(E_{xc}\) 的精确定义。它是一个“垃圾堆”泛函，包含了所有真实系统与虚构 KS 系统之间的差异。

• \(E_{xc}[\rho] = (T_{true}[\rho] - T_s[\rho]) + (\langle \Psi_{true} | \hat{V}_{ee} | \Psi_{true} \rangle - E_{Hartree}[\rho])\)
  • 第一部分：\((T_{true}[\rho] - T_s[\rho])\)
    • 这是动能的关联部分 \(T_c\)。
    • \(T_{true}\) 是真实系统的（未知的）总动能。
    • \(T_s\) 是我们用 KS 轨道精确计算的无相互作用动能。
    • \(E_{xc}\) 必须包含这个动能差。
  • 第二部分：\((\langle \Psi_{true} | \hat{V}_{ee} | \Psi_{true} \rangle - E_{Hartree}[\rho])\)
    • 这是势能的交换与关联部分。
    • \(\langle \Psi_{true} | \hat{V}_{ee} | \Psi_{true} \rangle\) 是真实系统中电子-电子相互作用 \(\hat{V}_{ee}\) 的完整（未知的）期望值。
    • \(E_{Hartree}[\rho]\) 是我们可以精确计算的经典静电排斥能（哈特里能量）。
    • \(E_{xc}\) 包含了真实相互作用与经典排斥之间的差值，这部分就是纯粹的量子效应（交换 + 关联）。

一句话总结：\(E_{xc}\) 包含了所有我们不知道的动能和势能的复杂量子效应。

2. 核心公式：Kohn-Sham 总能量

有了 \(E_{xc}\) 的定义，Kohn-Sham 的总能量泛函现在可以被精确地（在形式上）写为：

\[E_{KS}[\rho] = \mathbf{T_s[\{\phi_i\}]} + \int d\vec{r} V_{ext}(\vec{r})\rho(\vec{r}) + \frac{1}{2}\iint d\vec{r}d\vec{r}' \frac{\rho(\vec{r})\rho(\vec{r}')}{|\vec{r}-\vec{r}'|} + \mathbf{E_{xc}[\rho]}\]

• \(T_s[\{\phi_i\}]\)：无相互作用动能（通过轨道精确计算）。
• \(\int V_{ext} \rho\)：外势能（例如原子核吸引，已知）。
• \(\frac{1}{2}\iint ...\)：哈特里能量（经典静电排斥，已知）。
• \(E_{xc}[\rho]\)：交换关联能（这是唯一需要近似的部分！）。

这是整个 KS-DFT 的基石。 我们成功地将一个无法解决的 \(T_{true}\) 问题，转化为了一个可以被近似的 \(E_{xc}\) 问题。

3. 推导：Kohn-Sham 方程

我们如何找到使 \(E_{KS}[\rho]\) 最小的轨道 \(\phi_i\) 呢？ 答案是使用变分法：我们对总能量 \(E_{KS}\) 求关于轨道 \(\phi_i^*\) 的泛函导数，并令其为零。

• \(\frac{\delta}{\delta\phi_i^*} \left( E_{KS}[\rho] - \sum_j \epsilon_j (\int |\phi_j|^2 d\vec{r} - 1) \right) = 0\)
  • 这就是带有约束条件（每个轨道必须归一化）的能量最小化。
  • \(\epsilon_j\) 是拉格朗日乘子。
• 对 \(E_{KS}\) 的每一项求导：
  • \(\frac{\delta T_s}{\delta\phi_i^*}\) \(\rightarrow\) \(-\frac{\hbar^2}{2m}\nabla^2 \phi_i(\vec{r})\)
  • \(\frac{\delta E_{V_{ext}}}{\delta\phi_i^*}\) \(\rightarrow\) \(V_{ext}(\vec{r}) \phi_i(\vec{r})\)
  • \(\frac{\delta E_{Hartree}}{\delta\phi_i^*}\) \(\rightarrow\) \(\left( \int \frac{\rho(\vec{r}')}{|\vec{r}-\vec{r}'|} d\vec{r}' \right) \phi_i(\vec{r})\) (即 \(V_H(\vec{r})\phi_i(\vec{r})\))
  • \(\frac{\delta E_{xc}}{\delta\phi_i^*}\) \(\rightarrow\) \(\left( \frac{\delta E_{xc}}{\delta\rho} \right) \phi_i(\vec{r})\) (即 \(V_{xc}(\vec{r})\phi_i(\vec{r})\))
  • \(\frac{\delta (\text{约束项})}{\delta\phi_i^*}\) \(\rightarrow\) \(\epsilon_i \phi_i(\vec{r})\)
• 把所有项合并，我们就得到了最终的 Kohn-Sham 方程： \[\left[ -\frac{\hbar^2}{2m}\nabla^2 + V_{ext}(\vec{r}) + \int \frac{\rho(\vec{r}')}{|\vec{r}-\vec{r}'|} d\vec{r}' + V_{xc}(\vec{r}) \right] \phi_i(\vec{r}) = \epsilon_i \phi_i(\vec{r})\]
  • \(\epsilon_i\)（拉格朗日乘子）的物理意义是 Kohn-Sham 轨道 \(\phi_i\) 的能量。

4. 结论：\(V_{KS}\) 的最终形式

Kohn-Sham 方程本质上是一个单粒子薛定谔方程 Ĥ_KS φ_i = ε_i φ_i。

通过上面的推导，我们明确地找到了这个虚构的 Kohn-Sham 势 \(V_{KS}\) 到底是什么：

\[V_{KS}(\vec{r}) = V_{ext}(\vec{r}) + V_H(\vec{r}) + V_{xc}(\vec{r})\]

\[V_{KS}(\vec{r}) = \underbrace{V_{ext}(\vec{r})}_{\text{原子核势}} + \underbrace{\int \frac{\rho(\vec{r}')}{|\vec{r}-\vec{r}'|} d\vec{r}'}_{\text{哈特里势 (经典排斥)}} + \underbrace{\frac{\delta E_{xc}[\rho]}{\delta\rho}}_{\text{交换关联势 (量子效应)}}\]

最终总结

这个方程完美地闭合了整个理论： * 我们想求解 \(V_{KS}\) 中的 \(\phi_i\)。 * 但 \(V_{KS}\) 本身又依赖于 \(V_H\) 和 \(V_{xc}\)。 * \(V_H\) 和 \(V_{xc}\) 又依赖于 \(\rho\)（密度）。 * 而 \(\rho\) 又是由 \(\phi_i\)（\(\rho = \sum |\phi_i|^2\)）构成的。

这是一个“鸡生蛋，蛋生鸡”的问题。 在实践中，我们必须通过自洽迭代 (self-consistent loop) 来求解： 1. 猜测一个初始密度 \(\rho_{in}\)。 2. 用 \(\rho_{in}\) 计算 \(V_H\) 和 \(V_{xc}\)，得到 \(V_{KS}\)。 3. 求解 KS 方程 \(\hat{H}_{KS} \phi_i = \epsilon_i \phi_i\) 得到新的轨道 \(\phi_i\)。 4. 用新的 \(\phi_i\) 计算出新的密度 \(\rho_{out} = \sum |\phi_i|^2\)。 5. 比较 \(\rho_{out}\) 和 \(\rho_{in}\)。如果它们不一致，就混合新旧密度，重复步骤 2。 6. 循环往复，直到 \(\rho_{out} = \rho_{in}\)，达到自洽，计算完成。

在前面，我们推导出了一切都取决于一个未知的、需要近似的能量项：交换关联泛函 \(E_{xc}[\rho]\)。

接下来展示的就是在实践中如何近似 \(E_{xc}[\rho]\) 的两种最基本、最重要的方法：LDA 和 GGA。

1. 局域密度近似 (Local Density Approximation, LDA)

这是对 \(E_{xc}[\rho]\) 最简单、最基础的近似。

• 图示： 白板左上角画了一个图：一个真实的、密度不均匀的分子（或固体），但在某一点 \(\vec{r}\) 处，我们“假装”它周围是一片均匀的电子海洋（自由电子气）。
• 核心思想 (LDA)： 系统在 \(\vec{r}\) 处的交换关联能量密度，仅仅取决于该点 \(\vec{r}\) 处的电子密度 \(\rho(\vec{r})\)。 我们假设它与具有相同密度的均匀电子气 (free electron gas) 的交换关联能量密度 \(\epsilon_{xc}^{unif}(\rho)\) 完全相同。
• 公式 1：\(E_{xc}^{LDA}[\rho]\) \[E_{xc}^{LDA}[\rho] = \int d\vec{r} \rho(\vec{r}) \epsilon_{xc}^{unif}(\rho(\vec{r}))\]
  • \(\epsilon_{xc}^{unif}(\rho)\)：这就是我们在第 3 张白板上推导过的均匀电子气的（单粒子）交换关联能量。这是一个已知的、关于 \(\rho\) 的函数（通过量子蒙特卡洛等方法可以精确算出）。
  • \(\rho(\vec{r})\)：该点的电子密度。
  • 含义： 我们在空间中逐点计算该点的 \(\rho\) 对应的 \(\epsilon_{xc}\)，然后乘以该点的密度 \(\rho\)，最后在整个空间积分（求和）。
• 公式 2：\(V_{xc}^{LDA}\) (交换关联势) \[V_{xc} = \frac{\delta E_{xc}}{\delta \rho} = \epsilon_{xc}(\rho, \vec{r}) + \rho(\vec{r}) \frac{\partial \epsilon_{xc}}{\partial \rho}\]
  • 这是将 \(E_{xc}^{LDA}\) 代入我们在第 5 张白板上定义的 \(V_{xc} = \delta E_{xc} / \delta \rho\) 中，通过链式法则推导出来的结果。
• “Perdew-Zunger (1981)”
  • 这是一个具体的 LDA 泛函的名称。Perdew 和 Zunger 在 1981 年利用高精度的均匀电子气数据（来自 Ceperley-Alder 的 QMC 计算），拟合出了一套非常精确和实用的 \(\epsilon_{xc}^{unif}(\rho)\) 参数化公式。这至今仍是 LDA 计算的标准。

2. 广义梯度近似 (Generalized-Gradient Approximation, GGA)

LDA 假设在 \(\vec{r}\) 处的能量只取决于 \(\rho(\vec{r})\)，这是一个非常强（且通常不正确）的假设。真实系统（如分子）的密度变化非常快。

• 核心思想 (GGA)： 一个更智能的近似，不仅要考虑该点的密度 \(\rho(\vec{r})\)，还应该考虑该点密度的变化率，即梯度的模 \(|\nabla\rho|\)。
  • 如果 \(|\nabla\rho|\) 很大，说明密度变化剧烈（如在分子键合区域或原子边缘），\(\epsilon_{xc}\) 应该与 LDA 不同。
• 公式 3：\(E_{xc}^{GGA}[\rho^\uparrow, \rho^\downarrow]\) \[E_{xc}^{GGA}[\rho^\uparrow, \rho^\downarrow] = \int d\vec{r} \rho(\vec{r}) \epsilon_{xc}(\rho^\uparrow, \rho^\downarrow, |\nabla\rho^\uparrow|, |\nabla\rho^\downarrow|, \vec{r})\]
  • \(\rho^\uparrow, \rho^\downarrow\)：自旋向上和自旋向下的电子密度（更完整的表述）。
  • \(|\nabla\rho^\uparrow|, |\nabla\rho^\downarrow|\)：新加入的项！ 密度梯度的信息被包含了进来。
  • \(\epsilon_{xc}(...)\)：现在是一个更复杂的函数，它不仅是 \(\rho\) 的函数，还是 \(|\nabla\rho|\) 的函数。
• “PBE”, “BLYP” …
  • 这些都是具体的 GGA 泛函的名称。它们就像 \(\epsilon_{xc}\) 的不同“配方”。
  • BLYP = Becke (交换) + Lee, Yang, Parr (关联)。
  • PBE = Perdew, Burke, Ernzerhof。
  • PBE 和 BLYP 是化学和材料科学中最常用、最成功的 GGA 泛函之二。

接下来介绍的是“Jacob’s Ladder”（DFT 近似的雅各天梯）的更高几层：meta-GGA 和 Hybrid functionals (混合泛函)。

1. 密度泛函近似 (DFA)

• DFA (Density Functional Approximation):
  • 这是一个总称，泛指我们对 \(E_{xc}[\rho]\)（交换关联泛函）所做的所有近似，包括 LDA, GGA 等。

2. Meta-GGA

这是超越 GGA 的“天梯”的下一级。

• \(\Delta\) meta GGA:
  • 核心思想： GGA 只用了 \(\rho\)（密度）和 \(|\nabla\rho|\)（密度梯度）。为了获得更高精度，meta-GGA 引入了第三种信息。
  • 成分：\(\rho, |\nabla\rho|, \nabla^2\rho? |\nabla\phi_i|^2\)
    • \(\rho\) (密度)
    • \(|\nabla\rho|\) (密度梯度)
    • ∇²ρ? (密度的拉普拉斯，一种可能的成分)
    • \(|\nabla\phi_i|^2\) (Kohn-Sham 轨道的动能密度 \(\tau\))：这是现代 meta-GGA 泛函中最关键的成分。它使得泛函间接地依赖于轨道，从而能“感知”更复杂的电子结构信息（例如，区分是单键、双键还是孤对电子）。
• “SCAN”
  • 这是一个具体的 meta-GGA 泛函的名称，是目前最流行、最成功的 meta-GGA 之一。

3. 一个关键问题：自相互作用误差 (SIE)

为什么我们需要更高级的泛函？因为 LDA 和 GGA 有一个根本性的缺陷。

• “self-interaction error” (自相互作用误差, SIE):
  • 问题来源： 在 DFT 中，一个电子的密度 \(\rho\) 是其自身的总密度 \(\rho\) 的一部分。在计算哈特里能量 \(E_H[\rho] \propto \iint \rho \rho' ...\) 时，这个电子错误地与它自己产生了静电排斥。
  • 本应： \(E_{xc}\)（交换能）应该完美地抵消掉这个虚假的自排斥。
  • 现实： LDA 和 GGA 泛函都未能完美抵消它。
• “charge too delocalized” (电荷过度离域):
  • 后果： 由于电子错误地“排斥”自己，系统为了降低能量，会倾向于将电子“涂抹”或“离域” (delocalize) 到尽可能大的空间中，以减小这种虚假的自排斥。
  • 图示： 白板上的山峰（或势垒）图示说明：SIE 导致电荷在过渡态的局域化（电子集中在某处）变得困难，因此 LDA/GGA 总是低估化学反应的能垒。
  • “Cl- — nH₂O”
    • 这是一个具体例子：一个 Cl⁻ 离子被水分子包围。LDA/GGA 会错误地将 Cl⁻ 上的负电荷“泄露”或“离域”到周围的水分子上，从而导致错误的体系结构和能量。

4. 解决方案：混合泛函 (Hybrid Functional)

这是“天梯”的第四级，是目前在化学计算中最标准、最常用的高精度方法。

• \(\Delta\) Hybrid functional:
  • 核心思想： 如何修复 SIE？
    • 我们知道，在 Hartree-Fock (HF) 理论中，其“交换能” \(E_x^{HF}\) 是通过轨道精确计算的，并且它完美地抵消了自相互作用。
    • 混合 (Hybrid) 思想： 让我们把 DFT (如 PBE) 的交换项拿掉一部分，替换为同一比例的“精确”的 HF 交换项。
• “PBE0” (一个具体的混合泛函名称):
  • 这是最著名的混合泛函之一。
  • \(E_{xc} = \frac{1}{4} E_x^{HF} + \frac{3}{4} E_x^{PBE} + E_c^{PBE}\)
  • 公式分解：
    • \(\frac{1}{4} E_x^{HF}\)：用 25% 的精确 HF 交换。
    • \(\frac{3}{4} E_x^{PBE}\)：用 75% 的 PBE (GGA) 交换。
    • \(E_c^{PBE}\)：用 100% 的 PBE (GGA) 关联。
  • 效果： 引入 25% 的精确交换，极大地纠正了自相互作用误差 (SIE)，使其在计算能垒、带隙、分子性质等方面远比纯 GGA 准确。

接下来介绍了当今计算化学和材料科学中最先进、最常用的几种高级泛函。

混合泛函 (Hybrid functional) 家族的“动物园”—— 它们是如何被构建的，以及它们各自解决了什么问题。

1. B3LYP (最著名的经验混合泛函)

• \(\Delta\) B3LYP:
  • 这是最著名的混合泛函之一，特别是在量子化学领域。
  • 它的构造是半经验的 (semi-empirical)，意味着它的混合参数是由拟合（fitting）一组精确的实验/基准化学数据（如分子的原子化热）而确定的。
• 公式： \[E_{xc} = E_x^{LDA} + a_0(E_x^{HF} - E_x^{LDA}) + a_x(E_x^{Becke} - E_x^{LDA}) + E_c^{LDA} + a_c(E_c^{LYP} - E_c^{LDA})\]
• 解释：
  • B3LYP (Becke, 3-parameter, Lee-Yang-Parr) 是一个复杂的“鸡尾酒”。
  • 它混合了 LDA 的交换和关联、Hartree-Fock (HF) 的精确交换，以及 GGA 的交换 (Becke88) 和关联 (LYP)。
  • a_0, a_x, a_c 是三个被拟合的参数，用于确定每种成分的“配比”。

2. 自洽混合泛函 (Self-consistent hybrid)

• \(\Delta\) Self-consistent hybrid:
  • 思想： 与其像 PBE0（固定 25%）或 B3LYP（经验拟合）那样指定一个混合参数 \(\alpha\)，我们是否能从第一性原理 (ab initio) 出发，让系统自己决定应该混合多少 HF 交换？
• 公式：
  • \(E_{xc} = \alpha E_x^{HF} + (1-\alpha) E_x^{GGA} + E_c^{GGA}\) (这与 PBE0 的形式相同)
• 关键创新：
  • \(\alpha = \frac{1}{\epsilon_\infty}\)
  • 解释： 混合比例 \(\alpha\) 被设定为材料高频介电常数 \(\epsilon_\infty\) 的倒数。
  • 物理意义： \(\epsilon_\infty\) 描述了材料中电子屏蔽 (screening) 库仑相互作用的能力。
    • 绝缘体/半导体：\(\epsilon_\infty\) 较小（例如 2-10），\(\alpha\) 较大（例如 10-50%），需要更多 HF 交换来打开带隙。
    • 金属：\(\epsilon_\infty \to \infty\)，\(\alpha \to 0\)，不需要 HF 交换（退化为纯 GGA）。
  • 这是一个自洽过程：\(\alpha\) 决定了电子结构，而电子结构（通过 GW 等理论）又决定了 \(\epsilon_\infty\)。

3. 范围分离混合泛函 (Range-separated hybrid)

• \(\Delta\) Range-separated hybrid:
  • 思想： 电子-电子排斥 \(1/r\) 在短距离和长距离下表现不同。也许我们不需要“一刀切”的混合。
  • 策略： 将 \(1/r\) 分割为短程 (short-range, SR) 和长程 (long-range, LR) 两部分，并对它们使用不同的泛函。
  • 旁边的涂鸦 ... ~ ... 和 screening（屏蔽）形象地说明了这种思想：在长程，相互作用被“屏蔽”了。
• 公式 (以 HSE06 为例):
  • 白板上写了 HSE06'（HSE 泛函的 2006 年版本），并给出了其参数：
  • \(\alpha = 0, \beta = 1/4\) (代入白板上那个复杂的通用公式)
• HSE06 泛函的通俗解释：
  • 它将 PBE (GGA) 泛函的交换部分 \(E_x^{PBE}\) 进行了范围分离：
  • 在短程 (SR): \(E_x = \frac{1}{4} E_x^{HF,SR} + \frac{3}{4} E_x^{PBE,SR}\)
    • (在短距离内，它是一个 PBE0 泛函，混合了 25% 的 HF 精确交换)
  • 在长程 (LR): \(E_x = E_x^{PBE,LR}\)
    • (在长距离处，它退化为 100% 的 PBE 纯 GGA 交换)
  • 关联部分 \(E_c\) 始终是 100% 的 PBE 关联。
• 为什么这样做？
  • 物理上： 修正了长程的自相互作用误差。
  • 计算上： 在固体 (solid) 计算中极其重要。HF 交换的计算量非常大，尤其是在长程。HSE 泛函通过在长程关闭HF 交换（即“屏蔽”它），使得计算速度大幅提升，同时保留了混合泛函在短程（如化学键）的高精度。

总结

1. 1 (HK 定理): 奠定了理论基石—— \(E = E[\rho]\)。
2. 2 (OF-DFT): 提出了理想的无轨道 DFT，并指出了其 \(T[\rho]\) 的困难。
3. 3 (自由电子气): 推导了 \(T[\rho]\) 的最简近似 \(T \propto \int \rho^{5/3}\)。
4. 4 (OF-DFT 求解): 展示了如何通过变分法 \(\delta E / \delta \rho = \mu\) 求解 \(\rho_0\)。
5. 5 (Kohn-Sham): 引入了实用方案 (KS-DFT)，用“轨道” \(\phi_i\) 精确计算动能 \(T_s\)，将未知项塞入 \(E_{xc}\)。
6. 6 (LDA/GGA): 展示了如何近似 \(E_{xc}\)（“雅各天梯”的第一、二层），即 LDA（依赖 \(\rho\)）和 GGA（依赖 \(\rho, |\nabla\rho|\)）。
7. 7 (Meta-GGA / Hybrid): 攀登天梯的更高层 (Meta-GGA, Hybrid-PBE0)，并指出了 LDA/GGA 的根本缺陷（自相互作用误差 SIE）。
8. 8 (B3LYP / HSE): 展示了最先进的泛函 (B3LYP, HSE06) 是如何通过经验拟合或范围分离等技巧，在精度和计算效率之间达到最佳平衡的。

这完整地勾勒出了 DFT 从 1960 年代的抽象理论到当今最前沿的计算工具的整个发展脉络。

PHYS 5120 - 计算能源材料和电子结构模拟 Lecture

Lecturer: Prof.PAN DING

密度泛函理论 (Density Functional Theory, DFT) 的核心概念笔记，这是一种在物理和化学领域，特别是量子化学和凝聚态物理中，用于研究多电子体系电子结构的计算方法。

密度泛函理论 (Density Functional Theory)

• N-electron (N 电子体系):
  • 波函数 (Wavefunction): \(\Psi(\vec{r}_1, \vec{r}_2, ..., \vec{r}_N): \mathbb{R}^{3N} \to \mathbb{C}\)
    • 这是一个包含 N 个电子的体系，其波函数 \(\Psi\) 是 \(3N\) 个空间坐标（每个电子有3个坐标）的函数，值域为复数 \(\mathbb{C}\)。这是一个非常高维度的复杂函数。
  • 电子密度 (Electron density): \(\rho(\vec{r}): \mathbb{R}^3 \to \mathbb{R}\)
    • 电子密度 \(\rho\) 只是空间中一点 \(\vec{r}\)（3个坐标）的函数，值域为实数 \(\mathbb{R}\)。
    • DFT 的核心思想就是用这个更简单的 \(\rho(\vec{r})\) 来代替复杂的 \(\Psi\) 作为基本变量。
• H.K. (Hohenberg-Kohn) 定理:
  • 这是 DFT 的理论基石。白板上的图示 ① 和 ② 总结了这两个定理。
  • 图示 ① (H.K. 第一定理):
    • Vext/H \(\leftrightarrow\) ρ(r) \(\leftrightarrow\) Ψi(r1, r2, ...)
    • 含义: 体系的外势 \(V_{ext}\) （通常指原子核对电子的吸引势，它决定了体系的哈密顿量 \(H\)）与基态电子密度 \(\rho(\vec{r})\) 之间存在一一对应关系。
    • 推论: 由于 \(V_{ext}\) 决定了波函数 \(\Psi\)，因此，基态电子密度 \(\rho_0\) 唯一地决定了基态波函数 \(\Psi_0\) 以及体系的所有性质。
  • 图示 ② (H.K. 第二定理):
    • min E[ρ(r)] → ρ₀, Egs
    • 含义: 能量泛函 \(E[\rho]\) （能量是电子密度的函数）在正确的基态密度 \(\rho_0\) 处取得最小值，这个最小值就是体系的基态能量 \(E_{gs}\)。
• Levy-Lieb 泛函 (Levy-Lieb functional):
  • 也称为 Levy 约束搜索 (constrained search) 泛函。这是对 H.K. 定理中能量泛函 \(E[\rho]\) 的一种更严格和普适的定义。
  • ρ ← Vext : v-representability
    • 这提出了一个问题：什么样的密度 \(\rho\) 可以对应于某个外势 \(V_{ext}\)？这被称为“v-可表征性”问题。
  • Δ (三角符号通常表示 “定义为”)
  • N (圆圈) \(\supset\) K (圆圈)
    • 这个符号旁边的字迹有些潦草，但结合上下文，这可能是在区分 N-representability（N-可表征性）和 v-representability（v-可表Vext表征性）。

能量泛函与计算

• 约束搜索 (Constrained search):
  • \(\int \rho(\vec{r}) d\vec{r} = N\)
    • 这是一个约束条件，即电子密度在全空间积分必须等于体系的总电子数 \(N\)。
• ① 能量泛函 \(E_{LL}[\rho]\) (Levy-Lieb):
  • \(E_{LL}[\rho] = \min_{\Psi \to \rho} \langle \Psi | \hat{T} + \hat{V}_{ee} | \Psi \rangle + \int d\vec{r} V_{ext}(\vec{r}) \rho(\vec{r})\)
  • 解释:
    • 这个公式定义了总能量 \(E\) 如何作为密度 \(\rho\) 的泛函。
    • 它分为两部分：
      1. \(\int d\vec{r} V_{ext}(\vec{r}) \rho(\vec{r})\): 电子在外势 \(V_{ext}\) 中的能量。这部分是已知的（如果 \(V_{ext}\) 和 \(\rho\) 已知）。
      2. \(\min_{\Psi \to \rho} \langle \Psi | \hat{T} + \hat{V}_{ee} | \Psi \rangle\): 这是 Hohenberg-Kohn 泛函 \(F_{HK}[\rho]\)（也常被称为 Levy-Lieb 泛函），它代表动能 \(\hat{T}\) 和电子-电子相互作用能 \(\hat{V}_{ee}\) 的总和。
    • 约束搜索 (min \(\Psi \to \rho\))： \(F_{HK}[\rho]\) 的值是通过搜索所有能够产生该密度 \(\rho\) 的波函数 \(\Psi\)，并从中找出使 \(\langle \hat{T} + \hat{V}_{ee} \rangle\) 最小的那个 \(\Psi\) 来确定的。这个泛函 \(F_{HK}[\rho]\) 是普适 (Universal) 的，因为它不依赖于 \(V_{ext}\)。
• ② 求解基态 (Finding the Ground State):
  • \(E_{gs} = \min_{\rho} E_{LL}[\rho]\)
    • 含义 (H.K. 第二定理的变分原理): 体系的基态能量 \(E_{gs}\) 可以通过最小化总能量泛函 \(E_{LL}[\rho]\) 来获得。
  • \(\rho_0 \to \{\Psi_0^{(1)}, \Psi_0^{(2)}, ...\} \Rightarrow V_{ext}\)
    • 含义: 当找到最优的基态密度 \(\rho_0\) 时，我们就同时确定了基态能量 \(E_{gs}\)。通过这个 \(\rho_0\)（以及它对应的波函数集合），原则上也可以反推出唯一确定它的外势 \(V_{ext}\)。

其他笔记

• \(p_i \propto e^{-\beta E_i / Z}\) finite temperature
  • 这是白板右下角的一行字，与上面的 DFT 主题略有不同。
  • 含义: 这描述的是有限温度 (finite temperature) 下的正则系综 (canonical ensemble)。
  • \(p_i\) 是体系处于能量为 \(E_i\) 的某个状态的概率。
  • \(\beta = 1 / (k_B T)\)，\(k_B\) 是玻尔兹曼常数，\(T\) 是温度。
  • \(Z\) 是配分函数 (Partition function)。
  • 这个公式（玻尔兹曼分布）是统计力学的基础，用于将 DFT 推广到 \(T > 0\) K 的情况（即 Mermin 泛函）。

总结

总结了密度泛函理论 (DFT) 的数学和物理基础，从 Hohenberg-Kohn 定理（能量和密度的一一对应及变分原理）讲到了 Levy-Lieb 的约束搜索构造方法，这是现代 DFT 理论的核心。右下角的笔记则暗示了如何将此理论推广到有限温度体系。

这是（基态 DFT）内容的延续，主题是有限温度和系综 DFT (Finite temperature and ensemble DFT)，以及无轨道 DFT (Orbital-free DFT)。

以下是白板上内容的逐条中文转录和解释：

有限温度和系综 DFT (Mermin DFT)

这部分内容将 DFT 从 \(T=0\text{K}\)（绝对零度，只关心基态）推广到 \(T > 0\text{K}\)（有限温度，需要考虑热激发和系综平均）。

• 对比 \(T=0\text{K}\) 和 \(T\) finite (有限温度):
  • \(T=0K\) (左栏):
    • \(\rho_0\) (基态密度)
    • \(|\Psi\rangle\) (基态波函数)
    • \(\langle \hat{O} \rangle = \langle \Psi | \hat{O} | \Psi \rangle\) (零温下的期望值)
  • \(T\) finite (中栏):
    • \(p_e\) (系综密度 / 热力学密度)
    • \(\hat{\rho} = \sum_i f_i |\Psi_i\rangle\langle\Psi_i|\) (密度矩阵)
    • \(\langle \hat{O} \rangle = \text{Tr}(\hat{\rho}\hat{O})\) (有限温度下的期望值，即系综平均)
• Mermin 泛函 (Mermin Functional):
  • 这是 Mermin (1965年) 对 DFT 的推广，用于描述有限温度下的体系。
  • 目标是最小化自由能 (Free Energy)，而不是总能量。
  • \(F_{Mermin}[\rho] = \min_{\hat{\rho} \to \rho} \text{Tr} \{ \hat{\rho} [ \hat{H} + \frac{1}{\beta}\ln\hat{\rho} ] \}\)
    • 解释:
      • 这里的 \(F\) 不是指 Hohenberg-Kohn 泛函，而是指亥姆霍兹自由能 (Helmholtz free energy) \(\Omega\)（或 \(A\)）。白板上写 \(F\) 可能是指普适泛函部分。
      • \(\hat{H}\) 是哈密顿量（不含 \(V_{ext}\) 的部分，即 \(\hat{T} + \hat{V}_{ee}\)）。
      • \(\frac{1}{\beta}\ln\hat{\rho}\) 这一项与熵 (Entropy) 相关 (\(S = -k_B \text{Tr}(\hat{\rho}\ln\hat{\rho})\))。
      • \(\beta = 1 / (k_B T)\)。
      • 整个 \(\text{Tr}\{...\}\) 表达式代表系统的亥姆霍兹自由能 \(A\)。
      • \(\min_{\hat{\rho} \to \rho}\)：与 Levy-Lieb 约束搜索类似，这里是搜索所有能产生密度 \(\rho\) 的密度矩阵 \(\hat{\rho}\)，并找到使自由能最小的那个。
• ② 自由能最小化:
  • \(F_e = \min_{\hat{\rho}_e} f_{mermin}[\rho], \rho_e\)
    • 这行字迹有些潦草，但结合上下文，它表达的意思是： 体系的平衡自由能 \(F_e\) (或 \(\Omega_e\)) 是通过最小化 Mermin 泛函得到的，此时对应的密度是平衡态密度 \(\rho_e\)。
  • \(\hat{\rho}_e = \frac{e^{-\beta \hat{H}}}{\text{Tr}(e^{-\beta \hat{H}})} = \frac{e^{-\beta \hat{H}}}{Z}\)
    • 这是热力学平衡态下的正则系综密度矩阵 (equilibrium density matrix)。\(Z\) 是配分函数。
  • \(\hat{H} = -\frac{1}{\beta}\ln(\hat{\rho}_e)\)
    • 这是上一个公式的简单变形，反解出哈密顿量 \(\hat{H}\)。
• 应用场景 (右上角):
  • \(T > 10,000K\) warm-dense materials
    • 指出这种有限温度 DFT 理论常用于研究温稠密物质 (WDM)，如行星核心或惯性约束聚变 (ICF) 实验中的状态。
  • Fermi sea (费米海):
    • 旁边的图示 (一个方框和坐标轴) 可能是在示意费米面在高温下变得模糊（即费米-狄拉克分布不再是 \(T=0\) 时的阶跃函数）。

칠 无轨道 DFT (Orbital-free DFT)

这部分回到了 \(T=0\) 的情况（或稍作修改也可用于有限温度），但介绍了一种计算上更简化的 DFT 方法。

• \(E[\rho]\) ?
  • 提出一个问题：能量泛函 \(E[\rho]\) 到底是什么样子的？
• \(\Delta\) Orbital-free DFT (OF-DFT):
  • 动机: Kohn-Sham DFT (标准的 DFT) 仍然需要求解一组单电子轨道，计算量随系统增大而急剧上升 (通常是 \(N^3\) 或更高)。OF-DFT 试图完全避免求解轨道，只依赖于密度 \(\rho\) 本身。
  • Thomas-Fermi-Dirac approximation (托马斯-费米-狄拉克 近似):
    • 这是 OF-DFT 中最早期和最简单的近似。
    • \(E_{TF}[\rho] = T[\rho] + \int V_{ext}(\vec{r})\rho(\vec{r})d\vec{r} + \frac{e^2}{2} \iint \frac{\rho(\vec{r})\rho(\vec{r}')}{|\vec{r}-\vec{r}'|}d\vec{r}d\vec{r}' + E_{xc}[\rho]\) ?
    • 泛函的组成：
      1. \(T[\rho]\): 动能泛函。在 OF-DFT 中，最大的挑战就是找到 \(T[\rho]\) 的一个精确的、仅依赖于密度的表达式。Thomas-Fermi 理论给出了第一个近似（\(T_{TF}[\rho] \propto \int \rho^{5/3} d\vec{r}\)）。
      2. \(\int V_{ext}(\vec{r})\rho(\vec{r})d\vec{r}\): 外势能量 (与标准 DFT 相同)。
      3. \(\frac{e^2}{2} \iint ...\): 电子-电子相互作用的哈特里 (Hartree) 能量，即经典的静电排斥能 (与标准 DFT 相同)。
      4. \(E_{xc}[\rho]\) ?: 交换关联 (Exchange-Correlation) 能量。
         • 白板上在这一项后面打了一个问号，表示这部分也需要一个仅依赖于 \(\rho\) 的近似泛函（例如 Local Density Approximation, LDA，其中 \(E_x \propto \int \rho^{4/3} d\vec{r}\)）。
         • 当 \(E_{xc}\) 包含狄拉克 (Dirac) 的交换能近似时，就称为 Thomas-Fermi-Dirac (TFD) 理论。

总结

从 \(T=0\) 的基态 DFT 出发，探讨了两个进阶主题： 1. Mermin DFT: 如何将 DFT 框架从 \(T=0\) 的总能量 \(E\) 推广到 \(T > 0\) 的自由能 \(F\)，这对于描述高温系统（如温稠密物质）至关重要。 2. Orbital-free DFT: 一种计算上可能更高效（但目前精度较低）的 DFT 方法，它试图避免使用 Kohn-Sham 轨道，而是直接构建总能量（特别是动能 \(T[\rho]\)）作为电子密度的显式泛函。

Orbital-free DFT (OF-DFT) 是一种“理想中”的 DFT，而我们通常在实践中（例如在 Google 上搜索“DFT 计算”）谈论的几乎都是 Kohn-Sham DFT (KS-DFT)。

它们都基于相同的 Hohenberg-Kohn 定理，但实现这个定理的策略完全不同。

Kohn-Sham (KS) DFT：实用的妥协方案

KS-DFT 的天才之处在于它没有试图直接解决那个最棘手的 \(T[\rho]\)（动能泛函）。

1. 核心思想：引入“虚拟系统”

Kohn 和 Sham 提出：我们不去处理那个复杂、强相互作用的真实电子系统，而是构建一个虚拟的、无相互作用的电子系统。

这个虚拟系统被设计为恰好具有与真实系统完全相同的基态电子密度 \(\rho_0(\vec{r})\)。

2. 为什么这样做有好处？

• 对于无相互作用的系统，我们精确地知道如何计算其动能！
• 动能 \(T_s\) 就是所有虚拟粒子（称为 Kohn-Sham 轨道 \(\phi_i\)）动能的总和。
• 这个系统的波函数就是一个简单的斯莱特行列式（Slater determinant），密度 \(\rho(\vec{r}) = \sum_i^N |\phi_i(\vec{r})|^2\)。

3. Kohn-Sham 能量泛函

KS-DFT 将总能量 \(E[\rho]\) 重新划分为以下几项：

\[E_{KS}[\rho] = T_s[\{\phi_i\}] + \int V_{ext} \rho(\vec{r}) d\vec{r} + E_H[\rho] + E_{xc}[\rho]\]

• \(T_s[\{\phi_i\}]\): 无相互作用动能。这是通过求解轨道 \(\phi_i\) 来精确计算的，而不是作为 \(\rho\) 的泛函来近似。
• \(\int V_{ext} \rho(\vec{r}) d\vec{r}\): 外势能 (与 OF-DFT 相同)。
• \(E_H[\rho]\): 电子-电子静电排斥能 (Hartree 能量，与 OF-DFT 相同)。
• \(E_{xc}[\rho]\): 交换关联能。

4. 在 \(E_{xc}\) 中

现在，未知被藏在了 \(E_{xc}[\rho]\) 这一项里。它包含： 1. 交换能 (纯量子效应)。 2. 关联能 (电子如何相互“躲避”)。 3. 动能差：真实系统的动能 \(T\) 和我们计算的无相互作用动能 \(T_s\) 之间的差值 \((T - T_s)\)。

KS-DFT 的巨大成功在于：\(E_{xc}[\rho]\) 这一项（虽然仍然未知且必须近似）被证明比直接近似 \(T[\rho]\) 要容易得多！

KS-DFT 的工作就是求解一组单电子方程（Kohn-Sham 方程），找到轨道 \(\phi_i\)，从而构建 \(\rho\)，并计算总能量。

对比：Kohn-Sham DFT vs. Orbital-Free DFT

这张表格总结了两者最关键的区别：

总结

• OF-DFT 一个完全依赖于密度的理论，计算速度极快，但苦于找不到准确的动能泛函 \(T[\rho]\)。
• KS-DFT (标准方法) 是一个务实的“妥协”。它引入了轨道，用 \(T_s\) 这一项精确地处理了大部分动能，把更小的、更“好近似”的动能差 \((T-T_s)\) 连同交换关联能一起打包成 \(E_{xc}[\rho]\)。

当今几乎所有的 DFT 软件（如 VASP, Gaussian, QE）都是基于 Kohn-Sham 方案的。

这推导的是自由电子气 (free electron gas) 的动能泛函，这个结果是无轨道 DFT (OF-DFT) 和局域密度近似 (LDA) 的理论基础。

这内容承接了上一张图的 \(T[\rho]\)（动能泛函）问题，展示了如何为最简单的系统——均匀的自由电子气——推导出 \(T\) 和 \(\rho\) 的关系。

详解

左半部分：自由电子气的基本设定

1. 标题：free electron gas (自由电子气)
   • 这是一个理想化模型，假设电子在无外势（或均匀正电荷背景）中自由运动。
2. 薛定谔方程：
   • \(-\frac{\hbar^2}{2m}\nabla^2\Psi = E_k\Psi\)
   • 这是自由粒子的定态薛定谔方程，其解为平面波。
3. 波函数与能量：
   • \(\Psi_k = \frac{1}{\sqrt{\Omega}} e^{i\vec{k}\cdot\vec{r}}\) （平面波解）
   • \(\Omega = L^3\) （系统体积）
   • \(E_k = \frac{\hbar^2 k^2}{2m}\) （能量本征值，k 是波矢 \(k=|\vec{k}|\)）
4. PBC (周期性边界条件):
   • kx = 0, ±2π/L, ±4π/L, ...
   • 这说明 \(\vec{k}\) 矢量在“k空间”中不是连续的，而是形成一个晶格，每个点占据的体积是 \((\frac{2\pi}{L})^3\)。
5. 3D 状态填充 (费米球):
   • 图示为一个球体，半径为 \(k_F\)（费米波矢）。在 \(T=0\text{K}\) 时，所有 \(k < k_F\) 的状态都被电子填满。
   • 计算电子总数 \(N^\sigma\) (单一自旋):
     • \(N^\sigma = \frac{\text{费米球体积}}{\text{单个 k 态体积}}\)
     • \(N^\sigma = \frac{\frac{4}{3}\pi (k_F^\sigma)^3}{(\frac{2\pi}{L})^3} = \frac{\frac{4}{3}\pi (k_F^\sigma)^3}{(2\pi)^3/\Omega}\)

右半部分：推导 \(T[\rho]\) (动能泛函)

1. 关联 \(k_F\) 和密度 \(\rho\):
   • 从左侧公式整理可得：\(\rho^\sigma = \frac{N^\sigma}{\Omega} = \frac{(k_F^\sigma)^3}{6\pi^2}\)。
   • 假设系统是自旋非极化的（\(\rho^\uparrow = \rho^\downarrow\)），总密度 \(\rho = \rho^\uparrow + \rho^\downarrow = 2\rho^\sigma\)，且 \(k_F^\uparrow = k_F^\downarrow = k_F\)。
   • 代入可得：\(\rho = 2 \cdot \frac{k_F^3}{6\pi^2} = \frac{k_F^3}{3\pi^2}\)。
   • \(\Rightarrow (k_F)^3 = 3\pi^2 \rho\) (白板上的关键关系)
2. 费米能 (Fermi Energy):
   • HOMO/VBM → EF (在连续能带中，最高占据能级就是费米能 \(E_F\))
   • \(E_F = \frac{\hbar^2 k_F^2}{2m}\)
3. 计算总动能 \(T\):
   • 总动能 \(T\) 是所有电子动能的总和。在 \(T=0\text{K}\) 时，等于对费米球内所有状态的能量 \(E_k\) 进行积分。
   • \(T = T^\uparrow + T^\downarrow\)
   • 通过积分（白板上省略了积分步骤，直接用了熟知结论），可以得到平均动能 \(\langle E_{kin} \rangle = \frac{3}{5} E_F\)。
   • 因此，总动能 \(T = N \cdot \langle E_{kin} \rangle = N \cdot \frac{3}{5} E_F\)。
4. T 作为 \(\rho\) 的泛函 (最终推导):
   • 这是最关键的一步：将 \(T = \frac{3}{5} N E_F\) 中的 \(N\) 和 \(E_F\) 全部用密度 \(\rho\) 替换掉。
   • \(N = \int \rho(\vec{r}) d\vec{r}\) (电子总数)
   • \(E_F = \frac{\hbar^2 k_F^2}{2m} = \frac{\hbar^2}{2m} (3\pi^2 \rho)^{2/3}\) (将 \(k_F\) 用 \(\rho\) 替换)
   • 局域密度近似 (Local Density Approximation, LDA):
     • 我们假设一个真实系统（密度不均匀，\(\rho = \rho(\vec{r})\)）的总动能，可以通过在空间中每一点 \((\vec{r})\) 使用上述均匀电子气的结果，然后求和（积分）得到。
     • \(T[\rho] = \int (\text{电子数密度}) \cdot (\text{平均动能}) d\vec{r}\)
     • \(T[\rho] = \int \rho(\vec{r}) \cdot \frac{3}{5} E_F(\rho(\vec{r})) d\vec{r}\)
     • \(T[\rho] = \int \rho(\vec{r}) \cdot \frac{3}{5} \left[ \frac{\hbar^2}{2m} (3\pi^2 \rho(\vec{r}))^{2/3} \right] d\vec{r}\)
   • 整理后得到白板上的最终公式：
     • \(T[\rho] = \frac{\hbar^2}{m} \frac{3}{10} (3\pi^2)^{2/3} \int \rho^{5/3}(\vec{r}) d\vec{r}\)
     • 这被称为托马斯-费米 (Thomas-Fermi) 动能泛函。

总结

这展示了 \(T[\rho] \propto \int \rho^{5/3} d\vec{r}\) 这个著名公式的来源。

• 它为无轨道 DFT 提供了第一个（也是最简单的）动能泛函 \(T[\rho]\) 近似。
• 它也是局域密度近似 (LDA) 的基础。在 Kohn-Sham DFT 中，虽然 \(T_s\) (无相互作用动能) 是通过轨道精确计算的，但 \(E_{xc}\) (交换关联能) 里的交换能 \(E_x\) 也是用完全相同的逻辑（自由电子气模型）推导出来的（\(E_x[\rho] \propto \int \rho^{4/3} d\vec{r}\)）。

无轨道密度泛函理论 (Orbital-Free DFT) 的核心求解方程，它直接源自前面的推导。

如何通过最小化能量泛函来找到基态密度 \(\rho_0\)。

详解

1. 核心思想：约束下的最小化

• \(\frac{\delta}{\delta\rho} \left( E_{TF}[\rho] - \mu (\int \rho(\vec{r})d\vec{r} - N) \right) = 0\)
  • 这是一个使用“拉格朗日乘子法”的泛函求导（或称变分）方程。
  • 目的： 寻找使总能量 \(E_{TF}[\rho]\) 达到最小值的那个密度 \(\rho\)。
  • 约束： 这个最小化必须满足一个条件，即电子密度在全空间积分必须等于总电子数 \(N\)（即 \(\int \rho(\vec{r})d\vec{r} = N\)）。
  • \(\mu\) (mu): 就是为这个约束条件引入的“拉格朗日乘子”。

2. 欧拉-拉格朗日方程 (Euler-Lagrange Equation)

• 下面那一大长串方程，就是执行上面那行泛函求导 \(\frac{\delta}{\delta\rho}\) 后得到的结果，其形式为 \(\frac{\delta E_{TF}[\rho]}{\delta\rho} = \mu\)。
• 让我们逐项分解 \(\frac{\delta E_{TF}[\rho]}{\delta\rho}\)：
  • \(E_{TF}[\rho] = T[\rho] + E_{V_{ext}}[\rho] + E_H[\rho] + E_{xc}[\rho]\) (这是上一张白板中定义的总能量)
• 方程的各项：
  • 第一项：\(\frac{\hbar^2}{m} \frac{3}{10} (3\pi^2)^{2/3} \cdot \frac{5}{3} \rho^{2/3}\)
    • 这是对 动能泛函 \(T[\rho]\) 求泛函导数的结果。
    • \(T[\rho] = C_F \int \rho^{5/3} d\vec{r}\) (来自上一张白板)。
    • \(\frac{\delta T[\rho]}{\delta\rho} = C_F \cdot \frac{5}{3} \rho^{2/3}\)。
    • 这一项代表一种源自动能的“量子压力”。
  • 第二项：\(V_{ext}(\vec{r})\)
    • 这是对 外势能 \(E_{V_{ext}}[\rho] = \int V_{ext}(\vec{r}) \rho(\vec{r}) d\vec{r}\) 求导的结果。
    • \(\frac{\delta E_{V_{ext}}[\rho]}{\delta\rho} = V_{ext}(\vec{r})\)。
  • 第三项：\(+ e^2 \int d\vec{r}' \frac{\rho(\vec{r}')}{|\vec{r}-\vec{r}'|}\)
    • 这是对 哈特里 (Hartree) 能量 \(E_H[\rho]\) （电子间经典静电排斥能）求导的结果。
    • 这一项就是哈特里势 \(V_H(\vec{r})\)，即 \(\rho\) 在 \(\vec{r}\) 处感受到的来自所有其他电子的静电势。
    • (注：白板上在 \(V_{ext}\) 和这一项之间写的 \(V_{exc}[\rho]\) 似乎是个笔误或简写，因为方程后面明确地分别写出了哈特里项和交换关联项。)
  • 第四项：\(+ \frac{\delta E_{xc}[\rho]}{\delta\rho}\)
    • 这是对 交换关联 (Exchange-Correlation) 能量 \(E_{xc}[\rho]\) 求导的结果。
    • 这个导数本身被定义为交换关联势 \(V_{xc}(\vec{r})\)。

3. 方程的物理意义

• \(= \mu \text{ chemical potential}\)
  • 方程表明，在基态密度 \(\rho_0\) 下，系统中所有“势”的总和在空间中处处等于一个常数 \(\mu\)。
  • 这个常数 \(\mu\)（拉格朗日乘子）的物理意义是体系的化学势 (chemical potential)，即向系统中添加一个电子所需的能量。

4. 总结

• \(\rho_0 \quad E_{TF}[\rho_0] \quad \text{shell}\)
  • \(\rho_0\): 通过求解上面那个复杂的（非线性）积分-微分方程，我们就能得到基态密度 \(\rho_0\)。
  • \(E_{TF}[\rho_0]\): 将 \(\rho_0\) 代回到 \(E_{TF}[\rho]\) 的原始表达式中，就能计算出体系的基态总能量。
  • \(\text{shell}\) (壳层): 这是一个非常重要的旁注。托马斯-费米 (Thomas-Fermi) 理论（即 OF-DFT 的最早版本）的一个著名缺陷是它无法预测原子中电子壳层结构（如 1s, 2s, 2p…）。它的密度 \(\rho\) 曲线是平滑的，没有“Kohn-Sham DFT”中轨道所产生的波峰和波谷。这个词很可能是在提醒这个理论的局限性。

整个系列总结

这四部分构成了一个关于 DFT 基础： 1. 1: 介绍了 DFT 的核心思想 (Hohenberg-Kohn 定理)，即能量是密度的泛函 \(E[\rho]\)。 2. 2: 探讨了两种 DFT 的实现：一种用于有限温度 (Mermin DFT)，另一种是无轨道 DFT (OF-DFT)，并写出了 \(E_{TF}[\rho]\) 的一般形式。 3. 3: 详细推导了 OF-DFT 中最关键的动能泛函 \(T[\rho] \propto \int \rho^{5/3} d\vec{r}\)，其基于自由电子气模型。 4. 4: 展示了如何使用这个 \(E_{TF}[\rho]\) 泛函，通过泛函求导（变分法）建立一个可解的方程（欧拉-拉格朗日方程），以求得基态密度 \(\rho_0\) 和能量 \(E_0\)。